定義
共軛數
共軛數
共軛數
共軛數
共軛數 共軛數 共軛數
共軛數如果，用代替 中的 所得到的數 叫做 的共軛數，注意若且唯若 是實數時， 。
相關性質定理
定理1
兩個複數之和的共軛數等於這兩個數的共軛數之和，兩個複數之積的共軛數等於每個因數的共軛數之積。
共軛數例如：如果 ，那么
共軛數
共軛數同樣
共軛數 共軛數 共軛數
共軛數如同與的對應(寫作 )，既在加法中又在乘法中被保持，叫做 自同構，實數域沒有自同構，除了每個數對應於它自己的這種平凡的情況，而複數域除了自己對應於自己和共軛關係的對應外，也沒有自同構。數學專業的大學畢業生將會一再遇到這個概念。
定理2
共軛數 共軛數
共軛數如果 具有實係數且 是一個複數， 那么 。
令
共軛數
共軛數
共軛數其中的 都是實數，從而 ，又
共軛數於是由定理1，
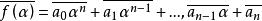共軛數
共軛數
共軛數
共軛數定理3
共軛數
共軛數
共軛數設是一個復係數多項式，而令 為每一個係數用它的共軛數代替後得到的多項式，那么 是一個實係數多項式。
如果
共軛數 共軛數
共軛數那么，中 的係數為
共軛數
共軛數
共軛數對於，有，由於它等於它自己的共軛數，所以是實數。
定理4
共軛數 共軛數
共軛數如果具有實係數，且有一個根，那么也是它的根。
共軛數
共軛數
共軛數因為如果，那么，所以。
共軛數
共軛數由於只有當是實數的時候，才有，我們得到下面定理。
定理5
一個實係數方程的非實根成共軛對出現。
共軛數令，那么
共軛數 共軛數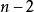 共軛數
共軛數其係數都是實的，這樣，如果一個n次實係數多項式有一個非實根，那么可寫成一個實的二次因式和另一個次實係數因式的積，繼續這樣論證下去證得下面定理。
定理6
每一個實係數多項式可以寫成若干個一次的或二次的實係數多項式的積。
主要有兩類共軛數
共軛無理數：形如a+√b和a-√b的，a、b為有理數，但b不是完全平方數的數互稱為共軛無理數。
共軛複數：複數範圍內，實部相同，虛部符號相反的，形如a+bi和a-bi的兩數互稱為共軛複數數。
以上兩種共稱為共軛數。
