概念
定義一
設G是一個平面圖,通過刪除G的一條邊(x,y),並且添加一個新結點a和兩條邊(x,a)與(a,y)(所獲得的任何圖也是平面圖)。這樣的操作稱為初等細分。若可以從相同的圖G通過一系列初等細分來獲得圖G₁和G₂,稱G₁和G₂是同胚的(homeomorphism)。
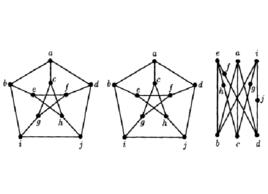
如圖1、2、3所示的三個圖G₁、G₂和G₃都是同胚的。
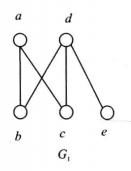 圖1
圖1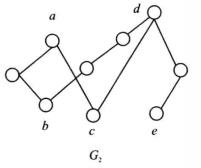 圖2
圖2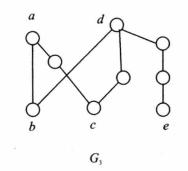 圖3
圖3定義二
設G=(V,E)是一個圖,e=uv是圖G的一條邊,w不是G的頂點,則當增加二度點w且用uw和vw代替邊e時,就稱邊e被細分.若圖H是由G經過一系列邊的細分而得到,則稱H為圖G的剖分圖(或細分圖).若兩個圖都是某一個圖的剖分圖,則這兩個圖稱為同胚的(或二度頂點內同胚).簡單圖G收縮邊wuv是將G的邊uv去掉,並將頂點u和v合併成一個新頂點.圖G可收縮成圖H.是指G可經過一系列的邊收縮而變成H.如果H是G的剖分圖,則G一定是H通過收縮一系列2度點所得到的收縮圖.
相關定理
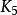 細分
細分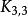 細分
細分Kuratowski定理 圖G是可平面的,若且唯若 和 的任何細分圖都不是G的子圖。
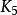 細分
細分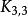 細分
細分根據對細分圖的描述,我們知道不僅 和 是不允許作為子圖出現的,而且它們的任何邊細分圖也是不允許的子圖,記住這一點很重要:違禁子圖不應被歸納出來。如果它們的確出現了,G就是不可平面的。
例題
例1 證明Peterson圖是不可平面的。
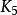 細分
細分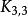 細分
細分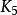 細分
細分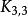 細分
細分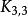 細分
細分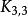 細分
細分證明 我們首先嘗試使用定理“如果G是n結點(n≥3)q邊的可平面圖,則q≤3n一6”。Peterson圖有q=15條邊和n=10個結點。代入定理中的不等式,我們得到15≤3(10)-6=24。非常遺憾,這條定理不起作用。滿足這個不等式並不能保證其可平面性,但是如果Peterson圖沒能滿足這個不等式,我們就能得出它是不可平面的。所以我們得換用另一個工具——"圖G是可平面的,若且唯若 和 的任何細分圖都不是G的子圖"。由於 的任何細分圖都有度為4的結點,且Peterson圖是3一正則圖,所以我們只需要尋找 的細分圖。圖4(a)是有標記Peterson圖,(b)是它的子圖同時也是 的細分圖,我們將這個子圖重畫為(c)以澄清它確實是 的子圖。因此,根據定理,Peterson圖的確是不可平面圖。
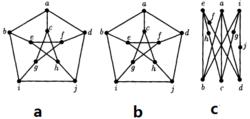 圖4
圖4例2 用Kuratowski定理說明圖5所示圖G不是平面圖。
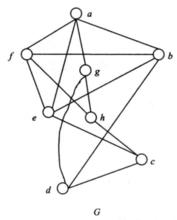 圖5
圖5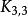 細分
細分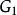 細分
細分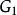 細分
細分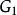 細分
細分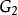 細分
細分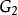 細分
細分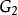 細分
細分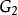 細分
細分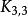 細分
細分解 將從圖G中找出一個同胚於 的子圖。圖G中結點a、b、f和e的度數均為4.刪去G中邊(a,b)與(f,e)得到圖G的一個子圖 ,且 中每個結點的度數均為3。再刪去圖 中邊(g,h)得到圖 ,圖 當然是圖G的子圖,且圖 中有兩個2度結點g與f,而圖 同胚於 ,因此圖G不是平面圖。
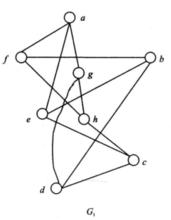 圖6
圖6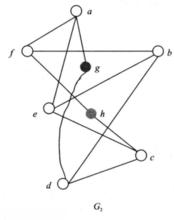 圖7
圖7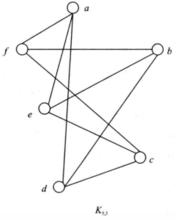 圖8
圖8