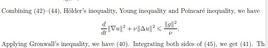一般形式
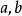 楊氏不等式
楊氏不等式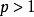 楊氏不等式
楊氏不等式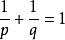 楊氏不等式
楊氏不等式假設是非負實數,, ,那么
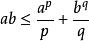 楊氏不等式
楊氏不等式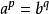 楊氏不等式
楊氏不等式等號成立若且唯若 .
加權形式
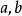 楊氏不等式
楊氏不等式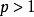 楊氏不等式
楊氏不等式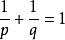 楊氏不等式
楊氏不等式假設是非負實數,,,那么
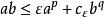 楊氏不等式
楊氏不等式 楊氏不等式
楊氏不等式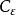 楊氏不等式
楊氏不等式其中任意小而任意大。
若且唯若 a=b時等號成立
Young不等式是加權算術-幾何平均值不等式的特例,Young不等式是證明Holder不等式的一個快捷方法
證明
1.若 b =0,不等式顯然成立。
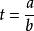 楊氏不等式
楊氏不等式若 b≠0, ,則該不等式變為
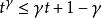 楊氏不等式
楊氏不等式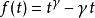 楊氏不等式
楊氏不等式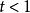 楊氏不等式
楊氏不等式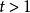 楊氏不等式
楊氏不等式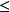 楊氏不等式
楊氏不等式設 , 時, f嚴格遞增, 時, f嚴格遞減,故f(t) f(1)=1-t,得證。
2.如果a>0且b>0,而數p,q滿足:1/p+1/q=1,那么
a^(1/p)*b^(1/q)≤(1/p)*a+(1/q)*b,當p>1
a^(1/p)*b^(1/q)≥(1/p)*a+(1/q)*b,當p<1
可以先證明:x>0時,
x^α-αx+α-1≤0,當0<α<1時;
x^α-αx+α-1≥0,當α>1時;
f(x)=x^α-αx+α-1
f'(x)=α[x^(α-1)-1],f'(1)=0
當0<α<1時;
當x∈(0,1);f'(x)>0;
當x∈(1,+∞);f'(x)<0;
∴f(x)在x=1處取最大值,又f(1)=0,∴f(x)≤0
當α>1時,
當x∈(0,1)時,f'(x)<0,
當x∈(1,+∞)時,f'(x)>0,
∴f(x)在x=1處取最小值,又f(1)=0,∴f(x)≥0
代入,x=a/b,α=1/p,得
f(a/b)=(a/b)^(1/p)-(1/p)*(a/b)+1/p-1
當p>1時,即0<α<1:
(a/b)^(1/p)-(1/p)*(a/b)+1/p-1≤0
即(a/b)^(1/p)≤(1/p)*(a/b)+1/q
同時乘以b,得:
a^(1/p)*b^(1/q)≤(1/p)*a+(1/q)*b
當p<1時,即α<0(p1(0<p<1)
(a/b)^(1/p)-(1/p)*(a/b)+1/p-1≥0即(a/b)^(1/p)≥(1/p)*(a/b)+1/q
同時乘以b,得:a^(1/p)*b^(1/q)≥(1/p)*a+(1/q)*b
證明2:令f(a)=a^p/p+b^q/q-ab,
f′(a)=a^(p-1)-b
令f′(a)>0,分2種情況
1、p>1,a>b^(1/(p-1))
f(a)>=f(b^(1/(p-1)))=0
即a^p/p+b^q/q>=ab
2、0<p<1,a<=b^(1/(p-1))
f(a)<=f(b^(1/(p-1)))=0
即a^p/p+b^q/q<=ab
證畢