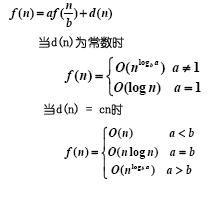計算
例如，在最短路徑問題中，設給定M個點1，2，…，M。點M是目的點，с>0是點i到點 j的距離i≠ j，с=0，i, j=1,2,…,M,要求出點i到點M的最短路。記ƒ(i)為從i到M的最短路長度。此問題的動態規劃基本方程為：
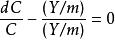策略疊代法其策略疊代法的程式如下：選定一初始策略 u(i)，在這問題中，策略 u(i)的意義是從點i出發走一步後到達的點，而且作為策略，它是集{1,2,…,M-1}上的函式。由 u(i)解下列方程組求出相應的值函式ƒ(i)：
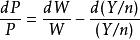策略疊代法再由ƒ(i)求改進的一次疊代策略 u(i)，使它是下列最小值問題的解：
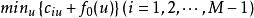策略疊代法然後，再如前面一樣，由 u(i)求出相應的值函式ƒ(i)，並由ƒ(i)求得改進的二次疊代策略 u(i)，如此繼續下去。
步驟
可見求解(1)的策略疊代法的程式由下列兩個基本步驟組成：
①求值計算 由策略 u(i)求相應的值函式ƒ(i)，即求下列方程的解：
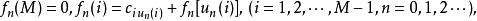策略疊代法②策略改進 由值函式ƒn(i)求改進的策略，即求下列最小值問題的解：
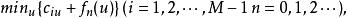策略疊代法式中規定，如 u(i)是上一問題的解，則取 u+1(i)= u(i)。
在一定條件下，由任選的初始策略出發，輪換進行這兩個步驟, 經有限步 N後將得出對所有i， uN+1(i)= uN(i)這樣求得的 uN(i)就是最優策略，相應的值函式ƒN(i)。是方程(1)的解。
對於更一般形式的動態規劃基本方程
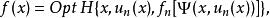策略疊代法這裡ƒ， H，φ為給定實函式。上述兩個步驟變成：
①求值計算 由策略 u( x)求相應的值函式 ƒ( x)，即求方程 之解， n=0，1，2…。
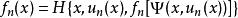策略疊代法②策略改進 由值函式ƒn( x)求改進的策略 un+1( x)，即求最優值問題（圖8）的解。
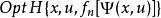策略疊代法對於滿足適當條件的方程(2)和初始策略，上述兩個步驟的解存在，並且在一定條件下，當 n→ 時，所得序列{ƒn( x)}與{ un( x)}在某種意義下分別收斂於(2)的解和最優策略。
策略疊代法最初是由R.貝爾曼提出的。1960年，R.A.霍華德對於一種馬爾可夫決策過程模型，提出了適用的策略疊代法，給出了相應的收斂性證明。後來，發現策略疊代法和牛頓疊代法在一定條件下的等價性，於是，從運算元方程的牛頓逼近法的角度去研究策略疊代法，得到了發展。
對於範圍很廣的一類馬爾可夫決策過程，其動態規劃基本方程可以寫成
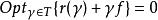策略疊代法式中ƒ∈ V，對所有 γ∈Γ:r(γ)∈ V，γ為 V→ V的線性運算元，Γ為這種運算元的族，而 V 則是由指標值函式所構造的函式空間。
假設 當 ƒ(γ)是方程 r(γ)+γƒ=0 的解時，它是對應於策略γ的指標值函式。
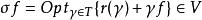策略疊代法最優策略，定義為最優值問題的解。
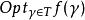策略疊代法這時由策略疊代法所求得的序列{fn}和{γn}滿足下列關係 ，其中的逆運算元。
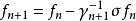策略疊代法當σ是加托可微時, γn+1是σ在ƒn處的加托導數。於是，上面的關係恰好表達了牛頓疊代法在運算元方程中的推廣。
解決問題
利用疊代算法解決問題，需要做好以下三個方面的工作：
一、確定疊代變數。在可以用疊代算法解決的問題中，至少存在一個直接或間接地不斷由舊值遞推出新值的變數，這個變數就是疊代變數。
二、建立疊代關係式。所謂疊代關係式，指如何從變數的前一個值推出其下一個值的公式（或關係）。疊代關係式的建立是解決疊代問題的關鍵，通常可以使用遞推或倒推的方法來完成。
三、對疊代過程進行控制。在什麼時候結束疊代過程？這是編寫疊代程式必須考慮的問題。不能讓疊代過程無休止地重複執行下去。疊代過程的控制通常可分為兩種情況：一種是所需的疊代次數是個確定的值，可以計算出來；另一種是所需的疊代次數無法確定。對於前一種情況，可以構建一個固定次數的循環來實現對疊代過程的控制；對於後一種情況，需要進一步分析出用來結束疊代過程的條件。
動態規劃
動態規劃是旦澤和貝爾曼提出的，他們關於這一定量化方法的重要著作發表於50年代。最初動態規劃指的是不確定性的線性規劃問題，而現在它已發展成為一個解決範圍廣泛的工商業務問題的定量技術了。
動態規劃的理論基礎為“最最佳化原則”。它是說一個最優策略是由最優子策略構成的。它可以定義為這樣的一個數學方法：它解決一串序貫決策問題，而這些決策中的每一個都又影響著未來的決策，且後面的決策對前面決策所決定的初始狀態來說總是最優的。這是非常重要的，因為我們很難遇到一個運行中的情況；其中的決策不影響未來的決策。經理們面對著的問題是要他們作出一系列決策，這些決策中的每一個都依賴於先前決策的結果。例如，一個生產經理可能為了得到眼前的高產量不顧未來的高產量而忽視工廠的維修工作。若每一決策只考慮它本身最最佳化，那么由全部決策所得到的收益可能不是最優的。相反如果在制定第1個或後續的決策時在收益上作些犧牲，雖然使各決策次最佳化了，但總的收益可能更高些。這就是動態規劃的目標。
一般說來，動態規劃處理的問題都含有時間變數。但是，它可以用來處理一些本來與時間無關的問題，這隻要在靜態模型中人為地引進“時間”因素，分成時段，把它看作多階段的動態模型就能用動態規劃的方法來解決了。
在很多領域中都有動態規劃的套用。如資源分配、貨物裝運、設備更新、生產計畫和存貯、排序、確定利息策略及評價投資機會等。
動態規劃可以看成是一個把複雜的大問題分成一系列較易解決的小問題的方法。它沒有標準的格式。
動態規劃模型有4個基本概念：(1)階段。它是所給問題中被劃分成若干個相互聯繫的時期或區間。(2)狀態變數。是表示某段的出發位置。這些狀態變數的值把制定決策需要了解的所有有關係統的情況都顯示出來。狀態變數數目可能很大，對於一定的計算能力，應盡能減少狀態變數的數目。(3)決策變數。表示狀態給定以後，從該狀態到下一階段某狀態的選擇。(4)目標函式。各個不同階段的決策能力，可能是距離、利潤、成本等。
