概念
函式疊代法(function iteration method)亦稱函式空間疊代。動態規劃的求解方法之一是以段數作為參變數,先求在各個不同段數下的最優策略,然後從對應的最優解中選出最優者,從而同時確定了最優段數。
 函式疊代法
函式疊代法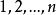 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法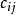 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法設有 個點: ,任意兩點 與 之間的距離(或行程時間,運費等)為 , 。 表示 與 為同一點, 表示兩點間無通路。由一點直接到另一點算作一步。要求在不限步數的條件下,找出點 到點 的最短路線。
我們把類似上述不限定數的有限階段決策問題稱為階段數不固定的有限階段決策過程。在解此問題時可以不考慮迴路,因為含有迴路的路線一定不是最短路。
 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法設 表示由點 到點 的最短距離,則由 最優性原理,得:
 函式疊代法
函式疊代法 函式疊代法
函式疊代法該方程是上述問題的動態規劃函式的基本方程。它是關於最優值函式的函式方程,而不是遞推關係式,這給求解帶來一定的困難,下面介紹求解該方程的函式疊代法。
 函式疊代法
函式疊代法 函式疊代法
函式疊代法函式疊代法的基本思想是構造一個函式序列 來逼近最優值函式 ,其算法步驟如下:
 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法:令
 函式疊代法
函式疊代法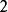 函式疊代法
函式疊代法 函式疊代法
函式疊代法:
 函式疊代法
函式疊代法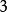 函式疊代法
函式疊代法 函式疊代法
函式疊代法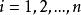 函式疊代法
函式疊代法 函式疊代法
函式疊代法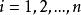 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法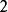 函式疊代法
函式疊代法:若,,則令,,停;否則,令,轉。
 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法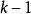 函式疊代法
函式疊代法 函式疊代法
函式疊代法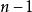 函式疊代法
函式疊代法算法中的意義十分直觀,表示由點出發,至多走步(即經過個點)到達點的最短路線的長度。因為不考慮迴路,所以算法的疊代次數一定不超過。
函式疊代法收斂性
 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法由函式疊代法的算法產生的函式序列關於單調下降且收斂到的解。
 函式疊代法
函式疊代法 函式疊代法
函式疊代法證明:任意的,有。
 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法取,則,故對皆成立。即關於單調下降。
 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法由,所以關於是單調有界序列,因而收斂,設收斂到,下面證明是的解。
 函式疊代法
函式疊代法 函式疊代法
函式疊代法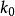 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法由於狀態僅取有限多個值,所以上述收斂是一致收斂。按定義,任給,總存在,當時,有,。
由此得:
 函式疊代法
函式疊代法從而
 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法令,由上面兩式有:
 函式疊代法
函式疊代法 函式疊代法
函式疊代法 函式疊代法
函式疊代法這表明收斂到方程的解。

