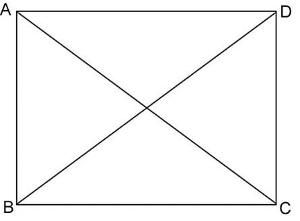
基本簡介
矩形(rectangle)是一種平面圖形,矩形的四個角都是直角,同時矩形的對角線相等,而且矩形所在平面內任一點到其兩對角線端點的距離的平方和相等。
 矩形
矩形 判定:
1.一個角是直角的平行四邊形是矩形。
2.對角線相等的平行四邊形是矩形。
3.有三個內角是直角的四邊形是矩形。
4.對角線相等且互相平分的四邊形是矩形。
說明:長方形和正方形都是矩形。平行四邊形的定義在矩形上仍然適用。
圖形學:
"矩形必須一組對邊與x軸平行,另一組對邊與y軸平行。不滿足此條件的幾何學矩形在計算機圖形學上視作一般四邊形。"在高等數學裡只提矩形,所以也就沒提長方形的長與寬。
詳細釋義
計算公式
面積:S=ab(注:a為長,b為寬)
周長:C=2(a+b)=2a+2b(注:a為長,b為寬)
外接圓
矩形矩形外接圓半徑 R=矩形對角線的一半
性質
 矩形
矩形 1.矩形的4個內角都是直角;
2.矩形的對角線相等且互相平分;
3.矩形所在平面內任一點到其兩對角線端點的距離的平方和相等;
4.矩形既是軸對稱圖形,也是中心對稱圖形(對稱軸是任何一組對邊中點的連線),它至少有兩條對稱軸。
5.矩形具有平行四邊形的所有性質
6.順次連線矩形各邊中點得到的四邊形是菱形
黃金矩形
寬與長的比是(√5-1)/2(約為0.618)的矩形叫做黃金矩形。
黃金矩形給我們一協調、勻稱的美感。世界各國許多著名的建築,為取得最佳的視覺效果,都採用了黃金矩形的設計。如希臘的巴特農神廟等。
判定套用
例1:已知ABCD的對角線AC和BD相交於點O,△AOB是等邊三角形,AB=4.求這個平行四邊形的面積。
分析:首先根據△AOB是等邊三角形及平行四邊形對角線互相平分的性質判定出ABCD是矩形(如圖個4-37),再利用勾股定理計算邊長,從而得到面積為
例2:已知:如圖4-38在ABCD中,M為BC中點,∠MAD=∠MDA.求證:四邊形ABCD是矩形.
分析:根據定義去證明一個角是直角,由△ABM≌DCM(SSS)即可實現。
例:3:已知:如圖4-39(a),ABCD的四個內角平分線相交於點E,F,G,H.求證:EG=FH.
分析:要證的EG,FH為四邊形EFGH的對角線,因此只需證明四邊形EFGH為矩形,而題目可分解出基本圖形:如圖4-39(b),因此,可選用“三個角是直角的四邊形是矩形”來證明
例4:已知:如圖 4-40,在△ABC中,∠C= 90°, CD為中線,延長CD到點E,使得DE=CD.連結AE,BE,則四邊形ACBE為矩形.