定義
設A,B都是n階矩陣,若存在可逆矩陣P,使P^(-1)AP=B,則稱B是A的相似矩陣, 並稱矩陣A與B 相似,記為A~B。
對進行運算稱為對進行 相似變換,稱可逆矩陣為 相似變換矩陣。
矩陣性質
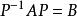 相似矩陣
相似矩陣對於
設 A, B和 C是任意同階方陣,則有:
(1)反身性: A~ A
(2)對稱性:若 A~ B,則 B~ A
(3)傳遞性:若 A~ B, B~ C,則 A~ C
(4)若 A~ B,則 r(A)=r(B),|A|=|B|,tr(A)=tr(B)。
(5)若 A~ B,且 A可逆,則 B也可逆,且 B ~ A。
(6)若 A~ B,則 A與 B
•兩者的秩相等;
•兩者的行列式值相等;
•兩者的跡數相等;
•兩者擁有同樣的特徵值,儘管相應的特徵向量一般不同;
•兩者擁有同樣的特徵多項式;
•兩者擁有同樣的初等因子。
(7)若 A與對角矩陣相似,則稱 A為可對角化矩陣,若 n階方陣 A有 n個線性無關的特徵向量,則稱 A為單純矩陣。
(8)相似矩陣具有相同的可逆性,當它們可逆時,則它們的逆矩陣也相似。
定理
定理1
n階矩陣 A與對角矩陣相似的充分必要條件為矩陣 A有 n個線性無關的特徵向量。
註: 定理的證明過程實際上已經給出了把方陣對角化的方法。
若矩陣可對角化,則可按下列步驟來實現:
(1) 求出全部的特徵值;
(2)對每一個特徵值,設其重數為k,則對應齊次方程組的基礎解系由k個向量構成,即為對應的線性無關的特徵向量;
(3)上面求出的特徵向量恰好為矩陣的各個線性無關的特徵向量。
推論1
若 n階矩陣 A有 n個相異的特徵值,則 A與對角矩陣相似。
對於 n階方陣 A,若存在可逆矩陣 P, 使其為對角陣,則稱方陣 A可對角化。
定理2
n階矩陣 A可對角化的充要條件是對應於 A的每個特徵值的線性無關的特徵向量的個數恰好等於該特徵值的重數,即設是矩陣 A的重特徵值。
定理3
對任意一個 n階矩陣 A,都存在 n階可逆矩陣 T使得即任一 n階矩陣 A都與 n階約當矩陣J相似。
判斷方法
判斷兩個矩陣是否相似的輔助方法:
(1)判斷特徵值是否相等;
(2)判斷行列式是否相等;
(3)判斷跡是否相等;
(4)判斷秩是否相等。
以上條件可以作為判斷矩陣是否相似的必要條件,而非充分條件。
(兩個矩陣若相似於同一對角矩陣,這兩個矩陣相似。)
套用
(1)利用矩陣對角化計算矩陣多項式;
(2)利用矩陣對角化求解線性微分方程組;
(3)利用矩陣對角化求解線性方程組。

