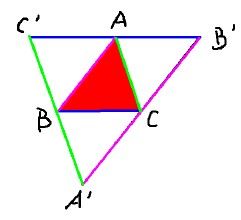
相似
數學上, 相似指兩個圖形的形狀完全相同。
嚴格來說,若存在兩個點的集,其中一個能通過放大縮小、平移或鏇轉等方式變成另一個,就說它們相似。
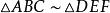 相似比
相似比兩個圖形相似,可以用一個“~”符號連線它們。例如,若三角形ABC和DEF相似,則可這樣表示:。
相似的特例是全等。
相似三角形
定義
對應角相等,對應邊成比例的三角形,叫做相似三角形。
【傳遞性】相似三角形的傳遞性:如果△ABC ∽ △A₁B₁C₁,△A1B1C1 ∽ △A₂B₂C₂,那么△ABC ∽ △A₂B₂C₂。
判定方法
(1)根據定義:對應角相等,對應邊成比例的三角形相似。
(2)根據平行線:平行於三角形一邊的直線和其他兩邊(或兩邊的延長線)相交,所構成的三角形與原三角形相似。
(3)判定定理1:兩角對應相等的兩個三角形相似(AA相似或AAA相似)。
(4)判定定理2:兩邊對應成比例且夾角相等,兩三角形相似(SAS相似)。
(5)判定定理3:三邊對應成比例,兩三角形相似(SSS相似)。
(6)直角三角形被斜邊上的高分成的兩個直角三角形和原三角形相似。
相似比性質
相似比是指兩個 相似圖形的對應邊的比值,這裡以相似三角形為例。
(1)相似三角形的一切對應線段(對應高線、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等於相似比;
(2)相似三角形周長的比等於相似比;
(3)相似三角形面積的比等於相似比的平方;
(4)相似三角形內切圓、外接圓直徑比和周長比都和相似比相同,內切圓、外接圓面積比是相似比的平方。
例題
在ABC中,DE∥BC,AD=EC,DB=1cm,AE=4cm,BC=5cm,求DE的長.
解:
 相似比
相似比∵ ,
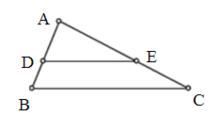 例一
例一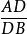 相似比
相似比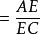 相似比
相似比∴ (平行於三角形一邊的直線截其他兩邊,所得的對應線段成比例)。
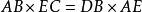 相似比
相似比∴,
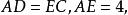 相似比
相似比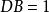 相似比
相似比又∵,
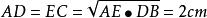 相似比
相似比∴。
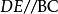 相似比
相似比又∵,
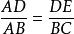 相似比
相似比∴ (平行於三角形一邊的直線和其他兩邊相交所構成的三角形與原三角形相似)。
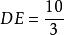 相似比
相似比∴。