相似論
正文
將描述物理現象的微分方程進行相似變換,以得到無因次數群之間的關係式的方法。它與因次分析方法一樣是一種指導實驗研究的方法,廣泛用於航空、航海、水利、建築等工程學科的實驗研究。在化學工程領域裡,它主要用於傳遞過程和單元操作的實驗研究,是對這些分支學科的形成和發展起過重要作用的一種化學工程研究方法。沿革 相似的概念起源於幾何學中。例如兩個三角形的對應角相等,則其對應邊長度之比值必相等,這兩個三角形稱為幾何相似。在幾何相似的系統中,若各對應點或對應部位上各相應物理量之比值相等,則這些系統為物理相似。
早在1686年I.牛頓就在《自然哲學的數學原理》一書中討論了流體運動相似的條件,並預見了相似論這一學科的創立。1822年,法國物理學家J.-B.-J.傅立葉在研究熱傳導時提出了熱相似的概念。但他們提出的流體運動相似和熱相似,都還只是就個別情況而言的。直到1848年法國J.貝特朗以力學方程式的分析為基礎,首次闡明了相似現象的基本性質,提出了相似第一定理,即凡相似的現象,其相似準數的數值相等。
此後,有許多學者將它套用於聲學、流體力學、航空動力學的研究,以相似準數的形式來處理實驗數據。英國科學家O.雷諾在研究管流的規律時,以雷諾數作為確定流動狀態為層流還是湍流的判據即為一例。後來俄國學者Α.費捷爾曼和美國學者E.白金漢分別導出了相似第二定理。該定理指出:可以用相似準數與同類量比值的函式關係來表示微分方程的積分結果。
1930年蘇聯科學家M.B.基爾皮契夫和A.A.古赫曼提出的相似第三定理指出:現象相似的充分必要條件是單值條件相似及由單值條件組成的相似準數相等。至此,相似論形成了一門完整的學科。
方法 在研究比較複雜的物理現象和工程問題時,人們往往通過建立微分方程和單值條件來描述各參數與變數間的關係。微分方程反映了一類過程的普遍規律,單值條件則規定了過程進行的具體條件,通常包括過程進行的空間範圍、參與過程物系的物理性質、過程在邊界上和時間上的特點等。相似論方法通過對微分方程和單值條件進行相似變換,得到若干與過程有關的物理量按不同組合構成的無因次數群,即為相似準數。在進行實驗研究時,應按相似準數的形式來測定和整理實驗數據。
例如,在研究流體在光滑水平直管中作定態流動的流動阻力時,單值條件為流體物性參數密度ρ、粘度μ以及幾何特徵參數管長l、管徑d;流速u、壓力p為非單值條件。描述這一流動問題的微分方程為:
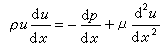
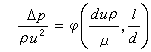
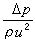 為歐拉數;
為歐拉數;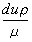 為雷諾數。
為雷諾數。 套用 一般說來,相似論的套用為:①在物理實驗中用相似準數的形式來處理實驗結果;②在工程試驗中按現象相似的條件,確定模型試驗的幾何條件和物理條件。
在化學工程領域裡,相似論有廣泛套用。描述動量傳遞、熱量傳遞、質量傳遞的基本規律的微分方程,如納維-斯托克斯方程(見運動方程)、能量方程、對流擴散方程等都早已建立。但迄今除某些比較簡單的情況外,這些方程一般無法求得解析解,甚至也不能得到數值解。化學工程研究者正是藉助於相似論的指導,對這些方程進行相似變換,得到與過程有關的相似準數,然後通過實驗研究確定相似準數間的函式關係,來探索這些傳遞過程的規律。如粘性流體流動的流動阻力,可用歐拉數與雷諾數的關係描述;強制對流傳熱的傳熱分係數,可用努塞爾數與雷諾數、普朗特數的關係描述;對流傳質的傳質分係數,可用舍伍德數與雷諾數、施密特數的關係描述。
對於一些比較複雜的化工問題,如在流態化研究中,可用弗勞德數作為區分散式流態化和聚式流態化的判據;在關於流化床的流體力學、傳熱、傳質研究中,也廣泛利用相似準數來處理實驗數據;在填充塔的操作性能的研究中,相似準數的關係式被用於液泛速度的計算。
與因次分析方法相比,相似論的結果更加可靠,因為它是通過微分方程的相似變換來求得相似準數的。但是當由於研究對象的複雜性難以確定微分方程和單值條件時,其套用就受到了限制。此外,對化學反應和物理變化共存的系統,因為不能同時滿足化學相似和物理相似的條件,相似論也不能奏效,這時可求助於數學模型方法。