定義
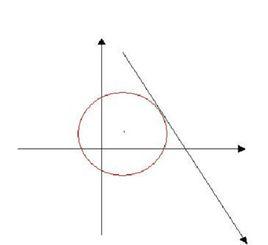
直線和圓有唯一公共點時,叫做直線和圓相切.
證明方法:(3種)
第一種
在直角坐標系中直線和圓交點的坐標應滿足直線方程和圓的方程,它應該是直線 Ax+By+C=0 和圓 x²+y²+Dx+Ey+F=0(D²+E²-4F=0)的公共解,因此圓和直線的關係,可由方程組
Ax+By+C=0
x²+y²+Dx+Ey+F=0
的解的情況來判別
如果方程組有兩組相等的實數解,那么直線與圓相切與一點,即直線是圓的切線。
第二種
直線與圓的位置關係還可以通過比較圓心到直線的距離d與圓半徑r的大小來判別,其中,當 d=r 時,直線與圓相切。
第三種
利用切線的定義 ——在已知條件中有“半徑與一條直線交於半徑的外端”,於是只需直接證明這條直線垂直於半徑的外端.
例: 已知:△ABC內接於⊙O,⊙O的直徑AE交BC於F點,點P在BC的延長線上,且∠CAP=∠ABC.
求證:PA是⊙O的切線.
證明:連線EC.
∵AE是⊙O的直徑,
∴∠ACE=90°,
∴∠E+∠EAC=90°.
∵∠E=∠B,又∠B=∠CAP,
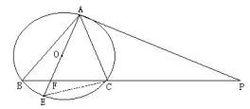 例題配圖
例題配圖∴∠E=∠CAP,
∴∠EAC+∠CAP=∠EAC+∠E=90°,
∴∠EAP=90°,
∴PA⊥OA,且過A點,
則PA是⊙O的切線.