基本介紹
某些幾何作圖，在分析、作圖的過程中、為了確定某點、某一線段、某一角度的相對位置，有時採用作一鋪助圓的方法，以使作圖問題求得簡化或解決之目的。此類方法稱為輔助圓法 。
舉例分析
【例1】求由兩個定點各作兩條射線，使交成一個正方形(本題要求:在二定點的連線上，不作垂線、不作平行線)。
已知 二定點A、B。
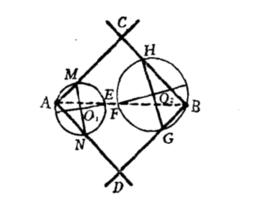
求作 射線AC、AD及BC、BD，使ACBD為一正方形(圖1)。
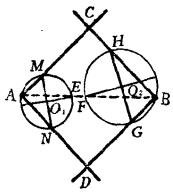圖1分析設正方形ACBD已經作成。
(1) 利用正方形的二對角線互為垂直、平分且相等的性質，本題很容易作圖。 但因有在AB連線上不作垂線，不作平行線的限制，只能另尋它法。
(2)若過A點作一適當大的圓O，交AB於E，交AC、AD於M、N，連MN、OE。因∠A=90°，知MN必過O點；因∠MAE=∠NAE=45°，知EO⊥MN；因E點可定，故知由E可定M、N二點。
(3) 同理可知，若過B點作一適當大的圓O，與BC、BD的二個交點H、G可由圓O與AB的交點F來定。有了MN、H、G四點，正方形ACBD可確定。
作法
(1) 作適當大的圓O，使過A點，交AB於E；作適當大的圓O，使過B點，交AB於F。
(2) 連OE，作直徑MN，使MN⊥OE；連OF，作直徑HG，使HG⊥OF。
(3) 由A點作射線AM、AN；由B點作射線BH、BG，得射線交點C、D。ACBD即為所求射線交成的正方形。
證明 據作圖MN⊥OE，HG⊥OF，知∠CAB= 45°，∠CBA=45°，則知△ACB是等腰直角三角形，AC = BC，∠C=90°；又因MN、HG是二圓的直徑，知∠A=90°，∠B=90°。顯見，四邊形ACBD因知二鄰邊相等、三個角為直角，必為正方形。故知從A、B二點所作射線符合作圖要求。
討論 本題總有一解 。
【例2】通過已知角內一定點求作一直線，使它截角的兩邊成周長一定的三角形。
已知 定長l及定角∠A內定點P (圖2)。
圖2作求 過P點的一直線，使截∠A形成的三角形的周長等於定長l。
分析 設直線BC已經作成，AB+BC+AC=l。設一圓O與BC相切於D，與∠A二邊相切於E、F二點。由圓的切線定理可知BD=BE，CD= CF，則知
AB+BC+AC=AB+BE+CF+AC=AE+AF=l，
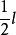輔助圓法作圖又因AE=AF，則知AE= AF=。
由此可見，E、F二點可定，則圓O可定，過P點向圓。
所作切線隨之而定。這條切線就是要求的直線。
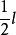輔助圓法作圖作法 (1) 在∠A二邊作AE=AF=；作圓O，使與∠A二邊相切於E、F二點。
(2)過P點作圓O的切線，交∠A二邊於B、C，直線BC即為所求。
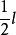輔助圓法作圖證明 設BC與圓O相切於D。因AE、AF、BC同為圓O的切線，知BD= BE，CD= CF，則知AB+ BC+ AC=AE+ AF，又因AE=AF=，故知AB+ BC+ AC=l。可見，過P點的直線BC符合作圖要求。
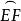輔助圓法作圖討論 當P點落在由AE、AF和小圍成的圖形內時，有二解；當P點落在該圖形上時(除A、E、F三點無解外)有一解；當P點落在該圖形外時，無解 。
