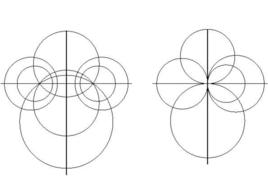
基本介紹
若一個圓集裡的圓兩兩的等冪軸是同一直線I，這圓集就叫做圓束，也叫做共軸圓系，l叫做圓束的等冪軸，圓束也就是同一平面內同時通過兩個定點的一族圓(這兩點可以為實點，也可以為虛點) 。
若已知圓束中的兩圓
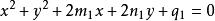共軛圓束和
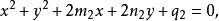共軛圓束則圓束的方程為
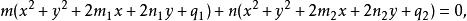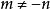共軛圓束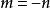
共軛圓束
共軛圓束其中m，n是參數， 。上述方程中，若 ，則方程表示一直線，該直線即圓束的等冪軸。
若圓束中所有圓都通過其中一圓與等冪軸的兩個交點，則稱這樣的圓束為橢圓型圓束。
若圓束中所有的圓都和等冪軸切於一點，則稱圓束為拋物線型圓束。
若圓束中所有的圓都和等冪軸無交點，則稱圓束為雙曲線型圓。
對於一個圓束，有無數多個圓與其中所有圓正交，這些圓之集合稱為已知圓束的 共軛圓束，橢圓型圓束與雙曲線型圓束共軛，拋物線型與拋物線型圓束共軛。
利用圓束可以研究等冪軸，亦可用來解決幾何作圖問題 。
相關結論
兩個圓束若具有性質：其中一個圓束中的每一個圓都與另一圓束中的每一個圓正交，則稱之為共軛圓束，每一個橢圓型圓東恰好有一個共軛圓束，它是個雙曲型圓束；反之，任一給定的雙曲型圓束的唯一共軛圓束總是橢圓型的。拋物型圓束則可配成共軛對 。
對於任意給定的兩個圓K₁和K₂，恰好存在一個同時含有它們的圓束，此圓束為橢圓型、拋物型或雙曲型乃是由所給兩圓有兩個交點、一個交點或沒有交點而定。
兩個相交或相切的圓總可以用適當的麥比烏斯變換，分別映照為兩條相交或平行的直線；兩個沒有公共點的圓，可以通過同樣的方法映照為兩個同心圓。
在一個圓束之中，總恰有一條直線，除非此圓束退化為同心圓或平行直線。事實上，這條直線是所給圓束之共軛圓束的圓心的軌跡。
在黎曼球面上球極投影為平面圓東的圓族可以用很簡單的措詞加以描述。因為，倘若我們考慮球面上的一個圓K，並過K的點Q作與K正交的球面切線，則所有這些切線必相交於空間一點P(也可以是∞)。反之，每一條過P的球面切線與球面相遇於K的點Q。但點P是K的平面(關於球面)的極。於是，球面上兩個圓互相正交，若且唯若一個圓的平面通過另一個圓的平面的極，並且反之亦然，亦即若且唯若它們的平面互為共軛時。
現在考慮球面上的兩個圓K₁和K₂，並設它們的平面的極分別是P₁和P₂，設g是聯結P₁和P₂的直線，通過g的平面束截球面得一族圓，它們在平面上的球極投影產生一個圓束，這個圓束將根據g與球面有兩個、一個或沒有交點而決定它是橢圓型的、拋物型的或雙曲型的，在以g為軸的平面束中，所有平面的極之軌跡是一條直線g’，直線g'可用以構造剛從g得到的圓束的共軛圓束 。
