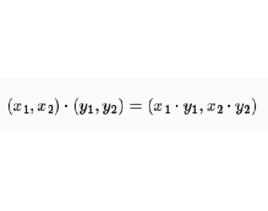直積簡介
 直積
直積 直積
直積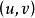 直積
直積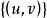 直積
直積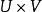 直積
直積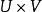 直積
直積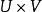 直積
直積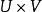 直積
直積對於兩個集合 U和 V,由 U的元素 和V的元素 的有序組 構成的集合 稱為 U和 V的直積集,記作 。當 U、 V具有像群、環等那樣的代數結構時,如果對 定義同樣的代數結構,則稱 是 U和 V的直積當 U、V具有拓撲結構時,可以通過對 定義適當的拓撲結構來定義 U和 V的直積。因為直積的概念是根據它的每個因子具有的結構在直積集中定義同樣的結構而產生的。所以它在數學的各個分支中都會出現。最簡單的例子是,可以把平面看作直線和直線的直積。群的直積、拓撲空間的直積、度量空間的直積、賦范線性空間的直積等都是重要的直積的例子。
不同種類的直積
群的直積
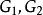 直積
直積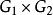 直積
直積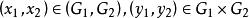 直積
直積設 是兩個群,在 上定義一個二元合成如下:對 ,令
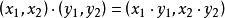 直積
直積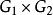 直積
直積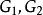 直積
直積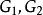 直積
直積關於這一合成構成群,稱為群 的 直積或 直積群。如果採用加法記號,則稱為群 的真和。
群的直積在群論研究中占有很重要的地位:群的外直積提供了由已知群構造新群的方法,群的內直積分解可把研究群G的結構化為研究其若干子群的結構,例如,任一有限生成交換群必可分解為若干循環子群的直積。
拓撲空間的直積
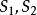 直積
直積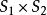 直積
直積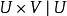 直積
直積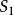 直積
直積 直積
直積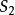 直積
直積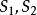 直積
直積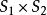 直積
直積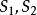 直積
直積設 是兩個拓撲空間,則 上以{ 是 的開集, 是 的開集}為基的拓撲,稱為 的拓撲的積拓撲,而賦予這一拓撲的直積 ,稱為拓撲空間 的直積。
度量空間的直積
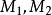 直積
直積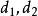 直積
直積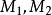 直積
直積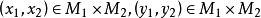 直積
直積設 是兩個度量空間, 分別是 上的距離,如果對 ,令
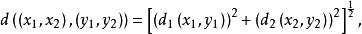 直積
直積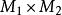 直積
直積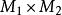 直積
直積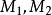 直積
直積則d是 上的一個距離函式。賦予這一距離的 ,稱為度量空間 的直積。
賦范線性空間的直積
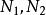 直積
直積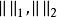 直積
直積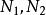 直積
直積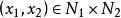 直積
直積設 是兩個賦范線性空間, 分別表示 上的範數。如果對 ,令
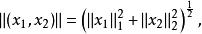 直積
直積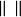 直積
直積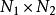 直積
直積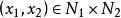 直積
直積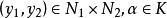 直積
直積則 是 上的—個範數。又對 , 。令
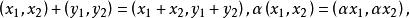 直積
直積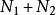 直積
直積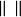 直積
直積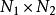 直積
直積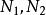 直積
直積則 又成為一個線性空間。連同方才定義的範數 , 成為一個賦范線性空間,稱為賦范線性空間 的直積。
矩陣的直積
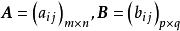 直積
直積設 ,稱如下的分塊矩陣
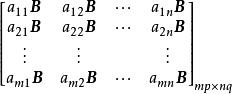 直積
直積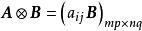 直積
直積為 A與 B的 直積( 張量積或 Kronecker 積),記為。
 直積
直積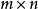 直積
直積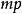 直積
直積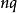 直積
直積 直積
直積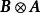 直積
直積 直積
直積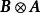 直積
直積由定義可知, 是一個 塊的分塊矩陣,它是一個 行 列的矩陣, 與 有相同的階數,但一般 ≠ ,即矩陣的直積不滿足交換律。
由直積的定義容易推出以下定理。
(1) 兩個上三角陣的直積也是上三角陣;
(2) 兩個對角陣的直積仍是對角陣;
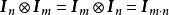 直積
直積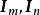 直積
直積(3) ( 為單位矩陣)。