釋義
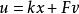狀態反饋狀態反饋是控制系統設計中的一種基本控制方式。給定線性定常系統Σ(A，B，C)，稱 為Σ的狀態反饋，其中K∈Rr×n，F∈Rr×r，且detF≠0。將上式代入原系統得閉環系統ΣC(A+BK，BF，C)。ΣC表明狀態反饋改變了原系統Σ的結構，因此也就改變了原系統的動態行為。狀態反饋不能改變原系統Σ的能控性，但能改變原系統Σ的能觀測性。
對系統Σ(A，B，C)，量測的通常不是全部狀態x而是輸出y。此時為實現狀態反饋必須增加狀態觀測器。為了直接套用量測信息，取u=Hy+Fv，其中H∈Rr×m，F同上，通常稱為輸出反饋。輸出反饋既不改變原系統Σ的能控性，又不改變原系統Σ的能觀測性。
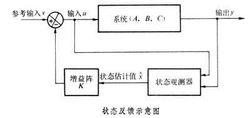狀態反饋圖中為狀態反饋的基本形式。其中是狀態變數的估計值，K是一個常係數矩陣（比例環節），通常稱為反饋增益矩陣。如果原系統是定常線性系統(A，B，C),則在引入狀態反饋K以後,系統就化成(A-BK，B，C)。狀態反饋把系統的動態矩陣A變成A-BK,但不影響輸入矩陣B和輸出矩陣C。狀態反饋也不影響系統的能控性，但可能改變系統的能觀測性。只要原系統是能控的，則一定可以通過適當選取反饋增益矩陣K用狀態反饋來任意移置閉環系統的極點(見極點配置)。對於傳統的輸出反饋,如果不引入附加的補償裝置，這一點不是總能作到的。
隨著狀態觀測器理論和狀態估計方法的發展（特別是由於卡爾曼-布希濾波方法的出現）,在很多情況下已不難獲得狀態變數的良好實時估計值，狀態反饋方法已進入了實用階段。
狀態反饋的描述式
對線性定常連續系統å(A,B,C),若取系統的狀態變數來構成反饋,則所得到的閉環控制系統稱為狀態反饋系統。狀態反饋閉環系統的系統結構可如下圖所示。
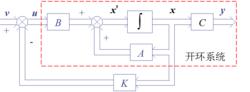狀態反饋系統的結構圖狀態反饋閉環系統的狀態空間模型可描述如下：
設開環系統狀態空間模型和狀態反饋律分別記為：
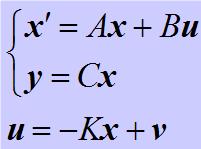狀態反饋其中K為r´n維的實矩陣,稱為狀態反饋矩陣;v為r維的輸入向量,亦稱為伺服輸入。將狀態反饋律代入開環系統方程, 則可得如下狀態反饋閉環控制系統的狀態空間模型:
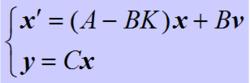狀態反饋狀態反饋閉環系統可簡記為åK(A-BK,B,C),其傳遞函式陣為:
GK(s)=C(sI-A+BK)-1B
狀態反饋對系統能觀測性的影響
狀態反饋對系統能觀測性的影響是指系統引入狀態反饋之後系統的能觀測性是否發生變化。例如，原系統是能觀測的，在引入狀態反饋之後，改變原來系統的能觀測性，同時也有可能出現相反的情況，即引入狀態反饋之後，原來不能觀測的系統變成能觀測的系統。
一般來說，當用狀態反饋配置的系統極點與原系統的零點相同，即出現零點、極點相消時，狀態反饋就改變了原來系統的能觀測性。
狀態反饋和輸出反饋的聯繫
控制理論最基本的任務是，對給定的被控系統設計能滿足所期望的性能指標的閉環控制系統，即尋找反饋控制律。狀態反饋和輸出反饋是控制系統設計中兩種主要的反饋策略，其意義分別為將觀測到的狀態和輸出取作反饋量以構成反饋律，實現對系統的閉環控制，以達到期望的對系統的性能指標要求。在經典控制理論中，一般只考慮由系統的輸出變數來構成反饋律，即輸出反饋。在現代控制理論的狀態空間分析方法中，多考慮採用狀態變數來構成反饋律，即狀態反饋。
之所以採用狀態變數來構成反饋律，是因為狀態空間分析中所採用的模型為狀態空間模型，其狀態變數可完全描述系統內部動態特性。由於由狀態變數所得到的關於系統動靜態的信息比輸出變數提供的信息更豐富、更全面，因此，若用狀態來構成反饋控制律，與用輸出反饋構成的反饋控制律相比，則設計反饋律有更大的可選擇的範圍，而閉環系統能達到更佳的性能。另一方面，從狀態空間模型輸出方程可以看出，輸出反饋可視為狀態反饋的一個特例。因此，採用狀態反饋應能達到更高的性能指標。
