牛頓-萊布尼茲公式
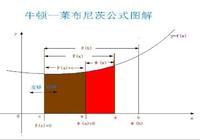
牛頓(Newton)-萊布尼茨(Leibniz)公式和圖解下面就是該公式的證明全過程:我們知道,對黎曼(Riemann)可積函式f(x)於區間[a,b]上的定積分表達為:b(上限)∫a(下限)f(x)dx現在我們把積分區間的上限作為一個變數,這樣我們就定義了一個新的函式:Φ(x)=x(上限)∫a(下限)f(x)dx但是這裡x出現了兩種意義,一是表示積分上限,二是表示被積函式的自變數,但定積分中被積函式的自變數取一個定值是沒意義的。雖然這種寫法是可以的,但習慣上常把被積函式的自變數改成別的字母如t,這樣意義就非常清楚了:Φ(x)=x(上限)∫a(下限)f(t)dt接下來我們就來研究這個函式Φ(x)的性質:命題1:定義函式Φ(x)=x(上限)∫a(下限)f(t)dt,則Φ(x)連續。當f(x)連續時,有Φ’(x)=f(x)。證明:讓函式Φ(x)獲得增量Δx,則對應的函式增量ΔΦ=Φ(x+Δx)-Φ(x)=x+Δx(上限)∫a(下限)f(t)dt-x(上限)∫a(下限)f(t)dt,利用區間可加性,x+Δx(上限)∫a(下限)f(t)dt-x(上限)∫a(下限)f(t)dt=x+Δx(上限)∫x(下限)f(t)dt若m和M分別是f(x)在區間[a,b]上的最小值和最大值,利用定積分第一中值定理,存在[m,M]中的實數η,使得ΔΦ=x+Δx(上限)∫x(下限)f(t)dt=η•Δx。進一步,當f(x)連續時存在x與x+Δx之間的常數ξ,使得η=f(ξ)。於是當Δx趨向於0時,ΔΦ趨向於0,即Φ(x)連續。若f(x)連續,那么當Δx趨向於0時,ξ趨向於x,f(ξ)趨向於f(x),故有limΔx→0ΔΦ/Δx=f(x),從而得出Φ’(x)=f(x)。命題2:若f(x)在[a,b]上連續,且F(x)是f(x)在[a,b]上的一個原函式,那么b(上限)∫a(下限)f(x)dx=F(b)-F(a)。證明:我們已證得Φ’(x)=f(x),故Φ(x)+C=F(x)。注意到Φ(a)=0(積分區間變為[a,a],故面積為0),所以F(a)=C,於是有Φ(x)=F(x)-F(a),當x=b時,Φ(b)=F(b)-F(a),這就得到了牛頓-萊布尼茨公式。注意:1)上述命題2中f(x)的連續性可以削弱為f(x)在[a,b]上Riemann可積,這個結論也稱為微積分第二基本定理,證明則相對複雜一些,需要從Riemann積分的定義出發來完成。2)f(x)是Riemann可積的不能保證f(x)的原函式F(x)存在,即不一定存在F(x)使得F'(x)=f(x),例子是Riemann函式。3)F(x)在(a,b)處處有有界導數不能保證F'(x)在[a,b]Riemann可積,例子是Volterra函式。《牛頓——萊布尼茲公式的圖解》——該公式的幾何(意義)說明多數人對,牛頓——萊布尼茲公式,是有一些誤解的。還是先看一看該定理的內容:設函式f(x)是閉區間[a,b]上的連續函式,F(x)是它在閉區間[a,b]上的任意一個原函式,則有:∫a↑bf(t)dt=F(b)-F(a)
首先,許多人都僅知道,y=f(x)是積分上限函式s=φ(x)=∫a↑xf(t)dt(a≤x≤b);在理解F(x)是它在閉區間[a,b]上的任意一個原函式,就出問題了!不會運用哲學的眼光看問題,並且對函式的理解也不到位。馬克思主義哲學指出:任何事物都與周圍的事物互相聯繫著。說F(x)是它在閉區間[a,b]上的任意一個原函式,是在一個特定的區間上[a,b]。可是在這個特定區間上,能夠滿足條件y=f(x)是其積分上限函式的函式多的是呢!而且它們的區間可以比[a,b]的要大一些。如圖S=F(x)=∫c↑bf(t)dt(c≤x≤b)所以說F(x)是它在閉區間[a,b]上的任意一個原函式,是指F(x)在閉區間[c,b]裡面的一部分子區間,即閉區間[a,b]。此圖,也可以做不定積分的一個直觀解釋。C是可以左右移動的,但不要超過a即(c≤a)
 公式圖解
公式圖解