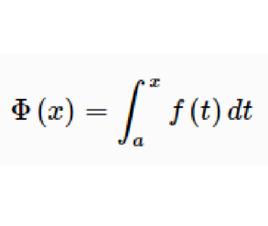積分上限函式

設函式y=f(x) 在區間[a，b]上可積，對任意x∈[a，b]，y=f(x)在[a，x] 上可積，且它的值與x構成一種對應關係（如概述中的圖片所示），稱Φ(x)為變上限的定積分函式，簡稱積分上限函式 。

定義

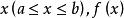積分上限函式

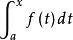積分上限函式

積分上限函式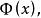

積分上限函式

設函式f(x)在區間[a，b]上可積，且對任意 在[a，x]上也可積，稱變上限定積分 為 的積分上限函式，記為 即

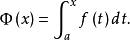積分上限函式

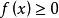積分上限函式

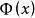積分上限函式

當 時， 在幾何上表示為右側鄰邊可以變動的曲邊梯形的面積(圖1中的陰影部分) 。

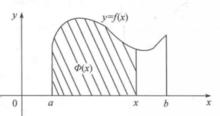圖1

定理

積分上限函式

設函式 在區間[a，b]上連續，則積分上限函式

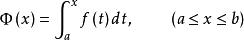積分上限函式

在[a，b]上可導，並且

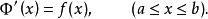積分上限函式

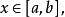積分上限函式

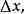積分上限函式

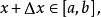積分上限函式

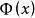積分上限函式

證明: 對於任意給定的 給x以增量 使得 由 的定義及定積分對區間的可加性，有

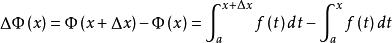積分上限函式

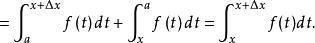積分上限函式

再由 定積分中值定理，得

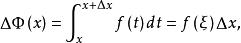積分上限函式

積分上限函式

積分上限函式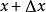

積分上限函式

其中， 在 和 之間。

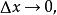積分上限函式

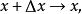積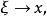分上限函式

積分上限函式

積分上限函式

令 則 從而 由 的連續性，得

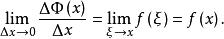積分上限函式

根據導數定義，得

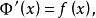積分上限函式

即

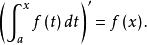積分上限函式

證畢。

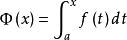積分上限函式

積分上限函式

這個定理說明，任何連續函式都有原函式存在，且積分上限函式 就是在[a，b] 上的一個原函式。上述定理也叫做 原函式存在定理 。