定義
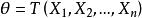 估計值
估計值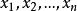 估計值
估計值 估計值
估計值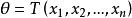 估計值
估計值估計值亦稱 估計量的實現,簡稱 估計,是指估計量的具體數值。在進行理論分析和一般性討論時,未知參數θ的估計量作為隨機樣本的函式,是隨機變數;在實際套用中,樣本是一組統計數據(隨機樣本的實現——樣本值),而估計量相應地取一具體值,即為θ 的估計值。
相關介紹
參數估計和測量平差都是利用有限個觀測的數值,遵循一定的原則,對母體中的未知參數進行估求,並在這個過程中要求觀測值的個數多於未知參數個數( 要有多餘觀測)。當然,觀測值個數越多,估計就越準確。
在數理統計中,當母體分布函式的形式為已知,但它的分布函式中的一個或多個參數卻是未知時,為了確定未知參數的值,就需要得到大量子樣觀測值,並用機率論對具有隨機現象的觀測值進行整理分析,從而去估計母體中未知參數的值,這個問題在數理統計中稱為 參 數估計。
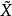 估計值
估計值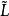 估計值
估計值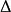 估計值
估計值平差問題是由於有多餘觀測而產生的,無論何種平差方法,其最終目的都是對參數真值和觀測值真值(或真誤差)作出某種估計,並評定其精度。所謂評定精度,就是對未知量的方差和協方差作出估計,我們將這種對未知量數值大小的估計和對未知量方差協方差的估計統稱為 平差模型的參數估計。
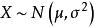 估計值
估計值 估計值
估計值 估計值
估計值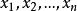 估計值
估計值 估計值
估計值 估計值
估計值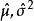 估計值
估計值在數理統計中,對未知參數的值進行估計的方法稱為 點估計( 也稱 定值估計)。設母體X的分布函式形式已知,如其中,參數(數學期望)、(方差)的真值或理論值未知,需對其進行估計。採用的方法為:通過獨立抽樣得到X的一組樣本觀測值(子樣),再按照某種原則構成適當的函式並將子樣觀測值代人計算,最終對母體中的未知參數( 或 )的值的大小進行估計,求得估值。這種方法稱為參數的 點估計法。
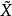 估計值
估計值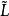 估計值
估計值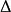 估計值
估計值綜上所述,測量平差的實質就是參數估計。平差中對參數和觀測值(或)的估計,就是點估計中對未知量的數學期望的估計;平差中對精度的估計,則是點估計中對方差和協方差的估計。在此應該強調:測量平差所遵循的基本原則,是最小二乘原則。最小二乘原則可認為是參數估計中最大似然原則的一種特殊情況,限於估計正態的母體均值。由最小二乘原得出白求平差模型參數的方法,稱為“最小二乘法”。最小二乘法最大的優點.就是在平差過程中可以抵禦觀測值含有的大量小誤差的影響.從而得到未知量的無偏估值,且估值的方差最小。也就是說,當觀測值中僅含有偶然誤差時,用最小二乘法可得到未知量的最優估值。
估計值的最優性質
點估計的關鍵在於找到上面所提到的“按照某種原則構成的適當的函式”,從而去對未知參數進行估計。這樣,“適當的雨數”並不是唯一的,因此就構成了不同的點估計法,常用的方法有矩法、最大似然法、子樣中位數法、截尾法等。對於同一個參數,用不同的方法來估計可能得到不同的估計量,而未知量的最優估計量( 也稱為最佳估計量)是估計量必須同時滿足無偏性、一致性和有效性的要求。下面討論這些性質的含意 。
無偏性
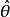 估計值
估計值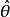 估計值
估計值估計量由隨機抽取的子樣決定,每一組子樣得到的估計量會由於隨機抽樣的影響而有,所不同,所以,估計量是隨機變數,我們希望估計量是在真值附近徘徊,隨著子樣容量n的增大,徘徊的幅度越來越小,亦即希望估計量的數學期望等於真值。所以,設未知參數的真值(理論值)為\hat{\theta },其估計量為,當滿足
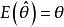 估計值
估計值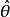 估計值
估計值 估計值
估計值時,稱為的 無偏估計量。
一致性
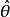 估計值
估計值 估計值
估計值 估計值
估計值一致性是要求參數估計量依機率收斂於。即對於任意小的正數,有
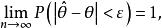 估計值
估計值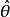 估計值
估計值其中,n為子樣容量。此外,若同時滿足
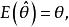 估計值
估計值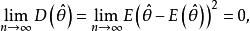 估計值
估計值 估計值
估計值 估計值
估計值則稱為的嚴格一致性估計量。嚴格一致性估計量一定是一致性估計量(有時證明某估計最滿足嚴格一致性反而要比證明它滿足一致性更方便一些)。
有效性
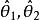 估計值
估計值 估計值
估計值設是的兩個無偏估計量,若
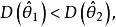 估計值
估計值 估計值
估計值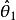 估計值
估計值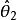 估計值
估計值則稱在估計時比更有效。
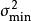 估計值
估計值 估計值
估計值 估計值
估計值 估計值
估計值 估計值
估計值此外,在所有對同一參數的無偏估計量中。各估計量的方差有一個下限,稱其為最小方差,所以,若有一無偏估計量,其方差滿足D()- =0,則認為是的 最有效估計量,稱為 最優估計量。
數理統計理論已經證明:具有無偏性、最優性的估計量必是一致性估計量,因此,在測量平差中,對參數估值的評選標準為最優和無偏,稱為 最優無偏估值 。

