定理定義
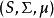 法圖引理
法圖引理 法圖引理
法圖引理設 為一個測度空間, 是一個實值的可測 正值函式列。那么:
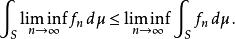 法圖引理
法圖引理其中函式極限是在逐點收斂的意義上的極限,函式取值和積分可以是無窮大。
驗證推導
 法圖引理
法圖引理定理證明基於單調收斂定理。設 為函式列的下極限。對每一個正整數 k ,要逐點定義下極限函式:
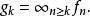 法圖引理
法圖引理 法圖引理
法圖引理所以是函式列 g1, g2, . . .單調遞增並趨於 。
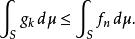 法圖引理
法圖引理任意 k ≤ n,有 g k ≤ f n,因此
據此,由單調收斂定理以及下極限定義,就有:
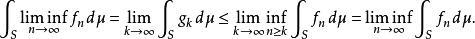 法圖引理
法圖引理反向法圖引理
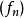 法圖引理
法圖引理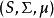 法圖引理
法圖引理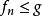 法圖引理
法圖引理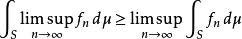 法圖引理
法圖引理令 為測度空間 中的一列的可測函式,函式的值域為擴展的實數軸(包括無窮大)。如果存在一個在 S上可積的正值函式 g ,使得對所有的 n都有 ,那么。
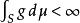 法圖引理
法圖引理這裡 g只需弱可積、即 。
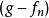 法圖引理
法圖引理證明:對函式列 套用法圖引理即可以。
定理推廣
任意實值函式
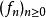 法圖引理
法圖引理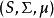 法圖引理
法圖引理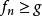 法圖引理
法圖引理法圖引理不僅對取正值函式列成立,在一定的限制條件下,可以擴展到任意實值函式。令 為測度空間 中的一列可測函式,函式的值域為擴展的實數軸(包括無窮大)。如果存在一個在 S 上可積的正值函式 g ,使得對所有的 n 都有 ,那么
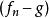 法圖引理
法圖引理證明:對函式列套用法圖引理即可。
逐點收斂
 法圖引理
法圖引理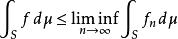 法圖引理
法圖引理在以上的條件下,如果函式列在 S上 μ-幾乎處處逐點收斂到一個函式,那么。
 法圖引理
法圖引理證明:是函式列的極限,因此自然是下極限。此外,零測集上的差異對於積分值沒有影響。
依測度收斂
 法圖引理
法圖引理如果函式列在 S上依測度收斂到,那么上面的命題仍然成立。
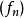 法圖引理
法圖引理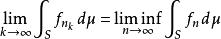 法圖引理
法圖引理證明:存在的一個子列使得。
 法圖引理
法圖引理 法圖引理
法圖引理這個子列仍然依測度收斂到,於是又存在這個子列的一個子列在 S 上 μ-幾乎處處逐點收斂到,於是命題成立。