馬爾法蒂問題

作法

Steiner於1826給出的作法：

1、作△ABC的三條角平分線，定出內心I；

2、作△IBC、△ICA、△IAB的內切圓，每兩個圓已有一條內公切線（分別為IC、IB、IA），再作另一條內公切線OP、QR、ST；

3、最後作圓與AB、AC、OP相切，作圓與AB/BC/QR相切，作圓與BC/CA/ST相切。

這三個圓即滿足要求。 Geometrikon

證明

幾個引理

引理一：
兩個相離的圓, 點P到兩圓的切線長度之差的絕對值為定值,
則點P的軌跡是一條二次曲線。
特別的 ：若點P到兩圓的切線長度之差的絕對值為兩圓內公切線之長度差，
那么點P的軌跡退化為雙直線 ，即兩圓的兩條內公切線。（證明過程略）
引理二：
三個圓兩兩相離， 若三條內公切線共點， 則另外三條內公切線也共點 。

證明 ：設三個圓為⊙A，⊙B，⊙C 。

記三個圓的三條內公切線交於Q。

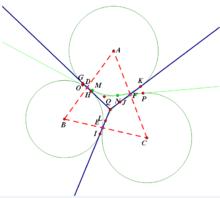圖1

QG切⊙A於G，又切⊙B於H，且交AB於D；

QI與⊙B和⊙C分別切於I， L，且與BC交於E ；

QJ與⊙C和⊙A分別切於J ，K，且與AC交於F。

設⊙A和⊙B的另一條內公切線切兩圓於M ，O ；

⊙A和⊙C的另一條內公切線切兩圓於N， P；

記MO和NP交於T 。

只須證明T也位於⊙B和⊙C的另一條內切線上。

證明如下，

因QDTF是⊙A的外切四邊形，

所以QD-QF=TF-TD 。

於是TP-TO=(TF+FP)-(TD+DO)

=(TF-TD)+FP-DO

=(QD-QF)+FJ-DH

=(QD-DH)-(QF-FJ)

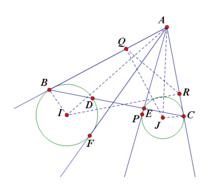圖2

=QH-QJ，

於是 ：T一定位於⊙B和⊙C的另一條內公切線上。

引理三：

給定⊙I和⊙J 及圓外動點A。

過A切⊙I於B和F， 切⊙J於C和P。

AP和AF位於AB和AC之間 。

BC與⊙I和J交於D和E。

求證：BD=CE的充要條件是∠BAF=∠CAP。

證明：記⊙J半徑為r1， ⊙I半徑為r2 ，∠BAJ=α ，∠CAI=β。

若BD=CE， 則B到⊙J的冪等於C到⊙I的冪 ，

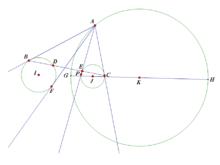圖3

於是：BJ^2-r1^2=CI^2-r2^2。

即：AB^2+AJ^2-2AB*AJ*cosα-r1^2=AC^2+AI^2-2AC*AI*cosβ -r2^2，

整理得：AB*AJ*cosα=AC*AI*cosβ 。
作JQ垂直AB於Q， 作IR垂直AC於R。
就有AB*AQ=AR*AC。
於是B Q R C共圓 ，又B I R A共圓 ，C J Q A共圓 。
所以∠AIR=∠ABR=∠ACQ=∠AJQ 。進而α=β。
所以∠BAI=∠CAJ ，
於是∠BAF=∠CAP。
反過來 ，當α=β時，由於上面的推理過程可逆，

故原題中的充要性是正確的。

Hart證明

馬爾法蒂問題（Malfatti's Problem）
在一個已知三角形內畫三個圓，每個圓與其他兩個圓以及三角形的兩邊相切。
Steiner於1826給出的作法：

1、作△ABC的三條角平分線，定出內心I；

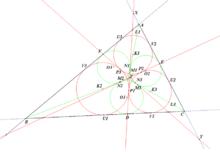圖4

2、作△IBC、△ICA、△IAB的內切圓，
每兩個圓已有一條內公切線（分別為IC、IB、IA），

再作另一條內公切線TF、TE、TE；

3、最後作圓與AB、AC、TF相切，
作圓與AB/BC/TD相切，
作圓與BC/CA/TE相切。
這三個圓即滿足要求。
由於Steiner未給出明確的證明，
後來由Hart給出了這個證明過程。證明：給定三角形ABC， 則一定存在滿足要求的三個圓。
設已經畫出了這三個圓 ：⊙K1切AB和AC於U3， V2 ；
⊙K2切BC和BA於U1 ，V3；
⊙K3切CB和CA於U2， V1；
⊙K1，⊙K2，⊙K3依次外切於P3，P1，P2；
三條內公切線交點記為T，則T為⊙K1 ⊙K2 ⊙K3的根心(等冪點)。

記TP1交BC於D， TP2交AC於E ，TP3交AB於F；
TP1和TP3交AC於X和Y。
三條直線TP1/TP3/AC所圍成的三角形的內切圓為⊙O2 ，
同樣的 ，TP1/TP2/AB的內切圓為⊙O3 ，
TP2/TP3/BC的內切圓為⊙O1 。
由於XE-YE=XU2-YV2=XP1-YP3=XT-YT ，
所以⊙O2切AC於E， 同理：⊙O3切AB於F ，⊙O1切BC於D。

記⊙O1和⊙O2切TP3於M3和N3,它們的另一條內公切線為L3;
⊙O2和⊙O3切TP1於M1,N1,它們的另一條內公切線為L1;
⊙O3和⊙O1切TP2於M2,N2,它們的另一條內公切線為L2;
設L1,L2和L3交於M。

下面證明L1經過點A.。
因為AE-AF=V2E-U3F=P3N3-P2M2=TN3-TM2=TM1-TN1，
又由於直線TM1N1是⊙O2和⊙O3的內公切線,
所以點A位於這兩圓的另一條內公切線上,
即：L1經過點A；同理：L2經過B；L3經過C。

下面證明L1平分∠BAC。
.因為FN3=FP3+P3N3=FU3+V2E=P2M2+P2E=EM2，
即F到⊙O2的冪等於E到⊙O3的冪，
所以L1平分∠A；同理：L2平分∠ B，L3平分∠C.。
M為三角形ABC的內心I。
至此Steiner關於Malfatti問題的作圖法證明完畢!