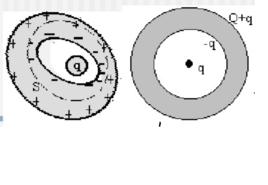
定理內容
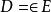靜電場唯一性定理靜電體系記憶體在電荷分布和電介質分布, 且關係式 成立, 如給定電荷分布和電介質分布, 整個邊界上給定下列件條之一或邊界上所有各部分分別給定下列條件之一
靜電場唯一性定理( 1 )電勢 ,
靜電場唯一性定理(2 )法線分量 , ·
靜電場唯一性定理
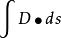靜電場唯一性定理(3 電勢 是一個未知常數，且電位移通量 =給定常數,
則體系的靜電場被唯一確定。
由上面所給唯一性定理, 直接可得出下面兩種形式的唯一性定理:
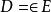靜電場唯一性定理 靜電場唯一性定理 靜電場唯一性定理( l) 靜電體系記憶體在電荷分布和電介質分布且關係式 成立，則體系的電場由電荷和電介質分布, 邊界上的 或 唯一確定。
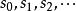靜電場唯一性定理
靜電場唯一性定理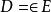 靜電場唯一性定理 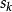靜電場唯一性定理
靜電場唯一性定理 靜電場唯一性定理( 2 ) 區域 由封閉曲面: 等包圍。如 內電荷分布和電介質分布給定, 且關係式 成立, 若在各邊界面上分別給定下列條件之一: ①s上電位給定, ②s上的電位移矢量的法線分量D 給定, ③ 為導體表面且總電荷給定. 則區域 內的電場被唯一確定.
以上唯一性定理對電介質分區均勻情況顯然成立。
論證過程
引理+疊加定理+證明
引理一：在無電荷的空間裡電勢不可能有極大值和極小值。
引理二：若所有導體的的電勢為0，則導體以外空間的電勢處處為0。
引理三：若所有導體都不帶電，則各導體的電勢都相等。
疊加定理：在給定各帶電導體的幾何形狀、相對位置後，賦予兩組邊界條件：
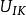靜電場唯一性定理
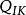靜電場唯一性定理1）給定每個導體的電勢 或總電量
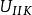靜電場唯一性定理
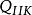靜電場唯一性定理2)給定每個導體的電勢 或總電量
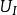靜電場唯一性定理
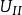靜電場唯一性定理
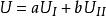靜電場唯一性定理設 、 滿足上述兩個條件，則他們的線性組合 必滿足條件三
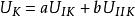靜電場唯一性定理
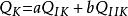靜電場唯一性定理3)給定每個導體的電勢或總電量
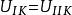靜電場唯一性定理
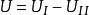靜電場唯一性定理特例：取,則(a=1,b=-1)
4)給定每個導體的電勢為0
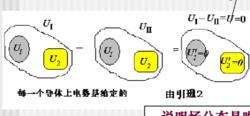靜電場唯一性定理理論推導其中，引理二和引理三可推論：所有導體都不帶電的情況下，空間各處的電勢和導體一樣，等於同一個常量。
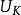靜電場唯一性定理 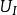靜電場唯一性定理 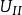靜電場唯一性定理
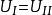靜電場唯一性定理
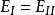靜電場唯一性定理由上可推出唯一性定理，給定每個導體電勢的情形，且設同一組邊值（k=1,2,...）有兩種恆定的電勢分布和，如下圖過程，便可得到即,因此推得唯一性定理。
至於唯一性定理的證明過程可查閱郭碩鴻的《電動力學》，這裡已經給出非常清晰的證明。
定理的套用
靜電場的唯一性定理可以用來直接或間接求解靜電場，如常用的試探法、鏡像法求解靜電場，而其他求解靜電場的常規方法如分離變數法和格林函式法，在求解靜電場時以解析法直接解場方程的方式得到場解，似乎無需用到唯一性定理，但實際求解時，唯一性定理的套用解決了所得解的正確性和唯一性的問題。以下以典型的靜電場求解問題為例闡明定理的套用和重要性靜電場的唯一性定理可以用來直接或間接求解靜電場，如常用的試探法、鏡像法求解靜電場，而其他求解靜電場的常規方法如分離變數法和格林函式法，在求解靜電場時以解析法直接解場方程的方式得到場解，似乎無需用到唯一性定理，但實際求解時，唯一性定理的套用解決了所得解的正確性和唯一性的問題。以下以典型的靜電場求解問題為例闡明定理的套用和重要性。
唯一性定理在鏡像法中的套用
鏡像法是求解靜電場邊值問題較為直觀的方法。在使用鏡像法求解靜電場時，鏡像電荷的設定和場解的具體形式必須在滿足唯一性定理的前提件下提出，即鏡像電荷不能放置在待求場區，否則影響場方程，解的形式除了滿足介質交界面上的銜接條件外，還要滿足其他邊界處的條件，這樣才能保證場解是唯一正確的。故唯一性定理的套用是鏡像法解題的核心思想之一。
唯一性定理在分離變數法中的套用
分離變數法是較為嚴格的數學解析求解場方程的方法。
在使用分離變數法得到靜電場場解的過程中，使用唯一性定理分析問題可以使解題思路明確，數學計算簡化，場解的唯一正確性得到理論上的保證。在教學過程中，分離變數法較為嚴格的數學解析過程較容易為學生接受，故如果先由分離變數法開始，分析唯一性定理的套用思想，深入剖析問題的物理本質，進而嘗試使用其他解法更容易令學生接受，在教學中會起到良好的效果。
唯一性定理直接求解靜電場
試探法是直接套用唯一性定理求解靜電場的方法。
試探法在靜電場邊值問題中的套用直接體現了唯一性定理在求解靜電場時的重要意義和價值。表現為當靜電場的場方程和邊界條件確定時，無論通過何種途徑得到的解，只要滿足場方程和邊界條件，所得解必為唯一正確的解。分析如下: 1) 提出適當的嘗試解的形式滿足場方程; 2) 場解的具體形式由邊界條件決定; 3) 無需嚴謹的數學推導，得到的場解必是唯一正確的。
唯一性定理解釋靜電禁止
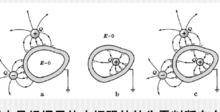唯一性定理解釋靜電禁止唯一性定理表明：一旦找到某種電荷分布既不違背導體平衡特性，又是物理實在，則這種電荷分布就是唯一可能的分布。如右圖所示。
關於此定理的套用需注意:
1) 在滿足唯一性定理的條件下，解是唯一的，但是不同情況下解的具體表述形式可以是不同的;
2) 區域的邊界條件可以分為3 種，第1 類為Dirichlet 邊界條件即給定邊界電勢; 第2 類為Neumann 邊界條件即給定邊界電勢的法嚮導數; 第3 類為混合邊界條件即已知一部分邊界電勢，已知一部分邊界電勢的法嚮導數。
