簡介
日食沙羅沙羅周期是日食和月食的周期，是指月球在它的軌道盤上運行一周（以便月球交點沿著軌道公轉一周）所需的時間——18年零10天。這個“Nordical”周期幾乎跟沙羅周期期間的一個太陰月(223 x 29.53 天= 6，585.19 天)的整數相等。因為沙羅周期的真正長度是6585.32天，因此你必須等三個沙羅周期，才能在地球上的相同地點看到日食再次發生。世界各地在沙羅周期中的連續食，有三分之一的是通過這種方式發生的，在3個沙羅周期後，即54年零33天后，日食幾乎又在相同的地理位置出現。12個不同的主要沙羅日食（Grand Saros eclipse）現在正在發生，其中一個的食分別發生在1937年、1955年、1973年、1991年和2009年，每一次食的持續時間都在7.5分鐘內。
沙羅周期是日食和月食的周期，是指月球在它的軌道盤上運行一周(以便月球交點沿著軌道公轉一周)所需的時間——18年零10天。
一個沙羅周期是6585 + 1/3 天（相當於18年11.3日或18年10.3日----如果有5個閏年），這是古巴比倫人對日食的觀測後發現的其周期性。“沙羅”是重複的意思，為18年零11天多一點。即6585．32天。
對全地球而言，一年內最多發生3次，有時1次也不發生，日食每年最多可發生5次，最少也要發生2次。
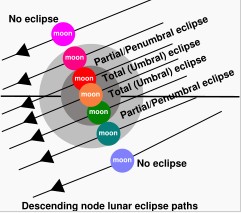發生在降交點附近的月食，屬於奇數列的沙羅序列。這種序列的第一個月食發生時，月球穿越地影的南緣，然後在每一次的沙羅周期中逐漸北移。這是由於日食帶的範圍小，地球上只有局部地區可見；對於某一確定地點而言，平均每3年左右才可以看到一次日偏食，300多年才可以看到一次日全食。而月食一旦發生，處於夜晚的半個地球上的人都可以看到，對某一地區平均而言，看到月食的機會是發生月食次數的一半，因此人們看到月食的機會比日食多。
“沙羅”一詞在拉丁語裡就是重複的意思，每個沙羅周期平均約有71次交食，包括日食43次，月食28次。有了沙羅周期，我們就可以預報月食了。例如1991年7月11日，發生了一次月全食，掩食帶穿過拉丁美洲及太平洋地區。人們往前推18年零11天，1973年6月30日一定也發生了一次日食，那次日全食的掩食帶橫穿了非洲大陸。如果往後推一個沙羅周期的時間，人們就能算出2009年7月22日也將發生一次日食，這就是即將發生在中國長江流域的日全食。
日食和月食統稱交食。由日月食的原理可看出，交食的出現與日、地、月三者的會合運動密切相關，此會合運動具有周期性，所以日月食自然也應有周期性。交食的周期是古代巴比倫人發現的，叫做“沙羅周期”（“沙羅”是重複的意思），為18年零11天多一點。即6585．32天。
由於地球繞太陽和月亮繞地球的公轉運動都有一定的規律，因此日食和月食的發生也具有其循環的周期性。有了沙羅周期，人們就可以預報日食了。例如1991年7月11日，發生了一次日全食，掩食帶穿過拉丁美洲及太平洋地區。人們往前推18年零11天，1973年6月30日一定也發生了一次日食，查閱資料發現確有此事，那次日全食的掩食帶橫穿了非洲大陸。如果往後推一個沙羅周期的時間，人們就能算出2009年7月22日也將發生一次日食，這就是即將發生在中國長江流域的日全食。
歷史發現
月的周期便被稱為“沙羅”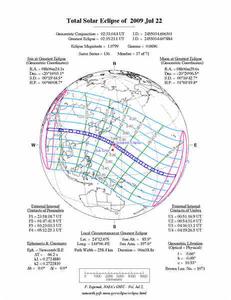
日食沙羅周期27.212220x242=6585.35724
29.530588x223=6585.32157
二者僅相差不到0.036日或50分鐘的成就。顯然這是非常了不起我國古代同樣也有值得驕傲的地方，也曾提出過多種類似的日月食規律。如漢代的《太初曆》中，就有一個“三統曆周期”，它長135個朔望月即3986.62965日，這與146.5個交點月 (3986.59023日)大致相等。在唐朝時，有位天文學家、數學家李淳風，他對日月食的預報已經十分嫻熟，相傳他在事先算出，貞觀八年五月辛未朔(公元634年6月1日)將有一次日全食後，按規定及時上奏了朝廷，可當時唐太宗對於這位年僅32歲的“太史令”還不夠信任，所以問道：“日或不蝕(食)，卿將何以自處?”李淳風胸有成竹，從容回答：“如不蝕(食)，臣請死之。”若不是有非常的把握，誰敢以自己的性命來作擔保?當然最後的結果是一場喜劇，有驚無險，但李淳風從此聲名大振，也獲得了唐太宗的充分信任。
性質說明
日食沙羅周期算法分析沙羅周期的起源是223個朔望月的時間長度大約與242個交點月相似，有與239個近點月接近 (大約只相差不到2小時)。這意味著經過一個沙羅周期，月球所經歷的朔望月、交點月和近點月幾乎都是整數，地球、太陽和月球三者的幾何關係幾乎完全一樣：月球在相同的交點上，有著相同的相位和與地球相同的距離。知道在某一天曾經發生一次食，則經過一個沙羅周期之際，幾乎一樣的食將再度發生。然而，沙羅周期 (18.031年)與月球的進動周期 (18.60年)並不相同，因此即使地球、太陽和月球三者的幾何關係幾乎完全一樣，但以恆星為背景的月球位置仍然不同。
沙羅周期的日數包含了⅓天的分數，不是整數使得問題更為複雜。由於地球的自轉使得使得經過完整的沙羅周期當天發生的食將延後約8個小時。在日食的情況下，這意味者能看見日食的區域將西移120°，或是三分之一個球面，因此在相同的地點上，每三次只能看見其中的一次。在月食的情況下，下一次的月食在相同的地點上看見月球在地平線上的時間可能是一樣的長，但如果等待三次沙羅周期 (54年1個月，幾乎大約就是19756日) 之後的月食會在當天幾乎相同的時間出現，這就是所謂的3沙羅周期或exeligmos （希臘語：“轉輪”）。
沙羅序列
沙羅算法每個沙羅序列由偏食開始，每經歷一個沙羅周期，月球的路徑就會向北移 (經過降交點的食) 或向南移 (經過升交點的食)。在某一個點上，食不再能夠發生，這個序列就結束了。在西元前2000年至西元3000年，每個序列大約持續1226年至1550年不等，每個序列有69至87次的日食，大多數都是71或72次。每個序列有39至59次中心食（多數是43次，包括全食、環食與全環食)。月食的序列沒有這么長，任何時間都有大約40個不同的沙羅序列在進行中。
無論月球在降交點或升交點 (日食或月食)，沙羅序列都以數字來編號。奇數的數字表示發生在接近升交點的日食，偶數的數字表示發生在接近降交點的日食；但在月食這種數字的搭配是相反的。沙羅序列的編號是以最大食出現，也就是最接近交點的時間來排列的。以2008年為例，共有39個 (117至155 ) 日食的沙羅序列在進行中，而月食則有41 (109至149 ) 個序列在進行中。
變化規律
沙羅周期沿著時間推移
沙羅發現者值得注意的是，19執政官年減去223個朔望月大約等於11個小時。這個長達11個小時的縫隙就是沙羅周期沿著時間推遲的原因。
假如把當前日蝕記做日蝕A，把一個沙羅周期後與之對應的的日蝕記做日蝕B，在任何
一個位置太陽和月球必須連成一條直線形成滿月。然而，太陽在B將不會回到離月亮交點相同距離的位置上(日蝕A時太陽的的位置)。在它完成那第19個19執政官年之前它有11個小時的路程。太陽在這11個小時中以平均27分鐘移動一弧度的速度移動(大約一度)，因此，日蝕B發生的位置便向西漂流0。5度(注意，日蝕發生的條件必須是太陽和月亮交點附近18度的範圍內)。
因為這個半度的漂移，沙羅周期也就有了開始和結束，在70到80次連續的日蝕後才會完全和以前重合。這樣，整個沙羅周期的循環就需要12到14個世紀的的時間。假設我們看見的日蝕是在月亮北交點東18度左右，此時的月球也在黃道的北邊1。5度。
月亮的陰影投在太陽北邊以至於僅僅和地球表面的北極地區檫邊而過，在北極附近形成一次日偏蝕。18年後的下一次日蝕將會多靠近月亮北交點半度左右，使月球的陰影向南移動。
日偏蝕將會是“比較深的”(更多的太陽被陰影覆蓋)，持續時間更長，在地球表面的覆蓋面積也更大。除此之外，月球陰影向地球赤道移動。最後，在10到11次日蝕之後，月亮的本影區投到地球上，引起一次日全蝕(或環蝕)。接下來的日蝕將全是日全蝕(或日環蝕)。
在赤道附近將會有整個沙羅家族中持續時間最長的日蝕發生(大約35到40次日蝕後，當日蝕發生點剛好在月亮北交點之後。整個日蝕將以相反的順序重複前一半的過程。在多個日全蝕之後，沙羅家族以10到11次日偏蝕在南極附近結束。最後，新月離月亮北交點太遠太遠，使得月亮的陰影不能投到地球表面，這次沙羅循環也因此結束。
如果日蝕在月亮南交點處發生，周期將是相同的，除非日蝕在南極發生並開始向北極移動。一個月蝕沙羅循環的推移情況也是相似的。
一次有多少個沙羅循環同時發生
正如我已經說過的，日蝕只發生在太陽處於月亮南北交點的前後18天內。這個長達一個月的時期叫做“日蝕季節”；期間可能發生一次到三次日蝕。而天空中的日蝕現象蝕非常頻繁的，所以事實上，每個日蝕季節都屬於不同的沙羅循環，月蝕沙羅循環也類似。
除此之外，隨著舊沙羅循環的逐漸消失，新的循環開始代替他，而且一直交迭下去。因此就有可能多個沙羅循環作用一個日蝕季節。
大體上，任何一段時間內，都會有38到42個太陽沙羅周期同時作用，月亮沙羅周期也一樣，每個都在他們各自的階段。因此，整個沙羅周期的結構是極其複雜的。
記數作用
沙羅算法天文上的沙羅周期記數方法是以van den Bergh出版的《a 1955 paper》為準，但忽視了一些至關重要的細節。他把起始於遙遠古代到現在的沙羅周期都做了編號。如果太陽靠近月亮北交點，沙羅就被編上奇數號，如果靠近南交點，沙羅就被編上偶數號。
太陽的沙羅循環和月球的沙羅循環分別編號(嚴格地按照太陽和月亮來區分)。。
占星家使用的沙羅數字相對更為複雜。第一，只看到過兩本討論沙羅周期的書，並且這兩本書都只講解了日蝕沙羅周期，月蝕沙羅周期則被忽略了。他們任意地為日蝕季節做連續編號為“1 North”(太陽在月亮北交點1度)，“1 South”(太陽在月亮南交點1度)。除此之外，如果兩次日蝕發生在相同的日蝕季節里(相隔29天)，前一個沙羅循環叫做“老”(old)和後一個沙羅家族叫做“新”(new)。這就使從公元727年開始的一個沙羅循環有了一個較長的名字，叫做“9 South Old”，而公元1917年開始的沙羅周期則被叫為“9 South New”。當舊的周期結束後，新的周期便再一次開始了，而先前的“new”也隨之換成了“old”。隨著周期的運轉，“new”也不停的更換，占星的編號方法就顯得更為複雜和混亂。
