水流能量方程

水流能量方程

正文

能量守恆與轉化定律在水或其他液體流動中的表達式。是水力學基本方程之一。液體在流動過程中各種機械能（動能、壓強勢能、位置勢能）之間相互轉化，同時克服水流阻力，要損耗一部分機械能，並等量地轉化為液體的熱能。這種機械能損失簡稱能量損失。非恆定流，既隨空間又隨時間而變化，能量關係複雜，一般僅就恆定流研究其能量守恆及轉化關係。
元流能量方程　對於恆定流，同一元流的任意兩個過水斷面之間或同一條流線上不同兩點之間的能量轉化關係，可表示為：

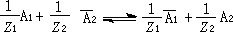(1)

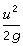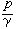式中u、p、z分別表示一點的流速、動水壓強和相對於基準面的高度；γ為液體容重；g為重力加速度；、、z 分別為單位重量液體的動能、壓強勢能和位置勢能（即重力勢能）；下標1、2表示該量屬於同一條流線上的點1或點2；h憜則為由點1到點2單位重量液體的能量損失。單位重量液體的能量具有長度的因次,習慣上,以水頭表示,故式(1)中各量又可稱為位置水頭、壓強水頭、流速水頭和水頭損失。實際液體在流動過程中總是有水頭損失，但在某些情況下，這種損失很小，可忽略不計，則方程(1)化為：

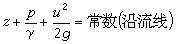　(2)

不同流線取不同常數，這就是著名的伯努利方程。該方程表明,當能量損失可略而不計時,液體的位置勢能、壓強勢能和動能沿流線可相互轉化，但總和不變，也就是機械能沿流線守恆。
總流能量方程　恆定總流過水斷面之間的能量轉化關係為：

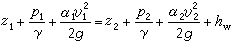　(3)

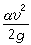式中v為斷面平均流速； 為斷面上單位重量液體的平均動能,即斷面流速水頭;hw為由斷面1流到斷面2的平均水頭損失； α為用斷面平均流速計算水流總能量時因過水斷面上流速分布不均勻而引進的恆大於 1的校正係數，稱動能校正係數。α 反映斷面上流速分布不均勻的程度，流速分布越均勻，α越接近於1。此外，1、2兩斷面必須是漸變流斷面(見圖)，通過斷面的流線近乎平行直線，斷面上任一點的位置勢能z與壓強勢能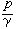之和等於常數，故(3)式兩端頭兩項可取斷面上任一點的值。若1、2斷面之間有能量H（按單位重量液體計）的加入或輸出(前者如水泵，後者如水輪機)，則在方程(3)左端加上或減去H。

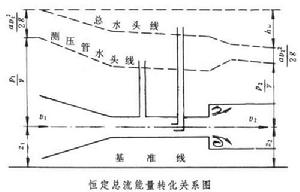水流能量方程

能量方程(3)中各項都具有長度的因次,採用幾何線段表示，更能形象地反映沿流能量轉化關係。如圖所示，由管壁開孔接通若干測壓管，管中液面到水平基準面的鉛直高度稱為測壓管水頭。沿流各斷面測壓管水頭連線稱測壓管水頭線。它沿流既可下降、也可上升。稱總水頭。沿流各斷面總水頭連線稱總水頭線。能量損失不可避免，流動一定朝著總水頭減小的方向，總水頭線只能沿流下降。沿流單位距離的水頭損失叫水力坡度。其表達式為：

(4)

式中s為沿流距離。
恆定流能量方程是水力學中套用最廣的基本方程。對許多流動問題均可套用能量方程建立起不同斷面各量（z、p、v等）之間的關係，再與水流連續性方程，或者還有水流動量方程聯立求解。套用能量方程的關鍵在於水頭損失項的計算，應注意選取符合相應實際情況的水頭損失係數值。

配圖

相關連線