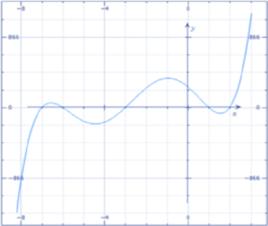
近代研究
拉格朗日的工作啟發了年輕的阿貝爾(挪威數學家),中學時期就自學了許多名家的數學著作,進大學後,開始研究五次方程的代數解問題。1824年,他嚴格地證明了高於四次的一般代數方程不可能有一般形式的代數解,這時他才22歲,尚未大學畢業,但沒有得到別人理解,將論文寄給高斯,也未引起注意,1826年才得以公開發表論文。阿貝爾只是證明了高於四次方程的一般代數方程不可能有一般形式的代數解,沒有指出哪些特殊的方程存在代數解。這個問題後來被法國年輕數學家伽羅瓦所解決,伽羅瓦創設的理論給出了可解性判別準則,並因此而開闢了數學的新領域—— 群論。
存在問題
二次、三次、四次方程的根都可以用它的係數的代數式(即只含有限項的加、減、乘、除和開方五種代數運算的表達式)來表示,五次及五次以上方程到底是否也行,這個問題吸引了眾多的著名數學家,在300多年的時間裡,人們的各種嘗試都失敗了。17世紀時英國數學家格里高利曾提出猜測:對於n>4的一般n次方程是不能用代數方法求解的,但沒有人能夠證明這個結論。
到了18世紀下半葉,法國數學家拉格朗日總結分析了別人失敗的教訓,也意識到這種用代數方法求解五次方程的公式可能不存在,構想了一種理論上的利用根式求解方程的步驟,但還是碰了壁。
一般常常認為,一般的五次方程沒有公式解存在,這是不正確的。利用一些超越函式,如 theta function 或 Dedekind eta function 即可找到五次方程的公式解。不存在的應當是根式解(即由方程的係數通過有限次的四則運算及根號組合而成的公式解)。另外,若我們只需要求得數值解,可以利用數值方法(如牛頓疊代法)得到相當理想的解答 。
布靈·傑拉德正規式
對於一般的五次方程式
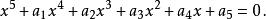 五次方程代數解
五次方程代數解可以藉由以下的轉換
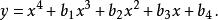 五次方程代數解
五次方程代數解 五次方程代數解
五次方程代數解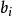 五次方程代數解
五次方程代數解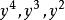 五次方程代數解
五次方程代數解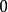 五次方程代數解
五次方程代數解得到一個 的五次多項式,上述的轉換稱為契爾恩豪森轉換(Tschirnhaus transformation),藉由特別選擇的係數 ,可以使 的係數為 ,從而得到如下的方程式:
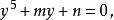 五次方程代數解
五次方程代數解以上的化簡方法是由厄蘭·塞繆爾·布靈所發現,後來喬治·傑拉德也獨立發現了此法,因此上式稱為 布靈·傑拉德正規式( Bring-Jerrard normal form)。 其步驟如下: 首先令
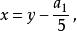 五次方程代數解
五次方程代數解可消去四次方項,得到
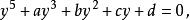 五次方程代數解
五次方程代數解其中,
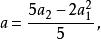 五次方程代數解
五次方程代數解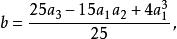 五次方程代數解
五次方程代數解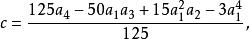 五次方程代數解
五次方程代數解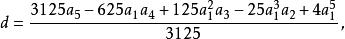 五次方程代數解
五次方程代數解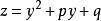 五次方程代數解
五次方程代數解接下來,令 , 得到
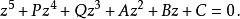 五次方程代數解
五次方程代數解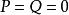 五次方程代數解
五次方程代數解再令 , 求得
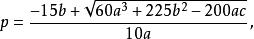 五次方程代數解
五次方程代數解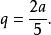 五次方程代數解
五次方程代數解第三步,利用契爾恩豪森想到的方法,令:
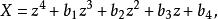 五次方程代數解
五次方程代數解代入
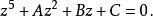 五次方程代數解
五次方程代數解得到
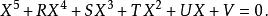 五次方程代數解
五次方程代數解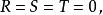 五次方程代數解
五次方程代數解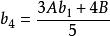 五次方程代數解
五次方程代數解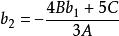 五次方程代數解
五次方程代數解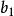 五次方程代數解
五次方程代數解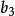 五次方程代數解
五次方程代數解再令 則得 , 若令 , 則 , 可由以下兩個方程解得:
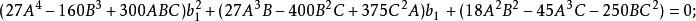 五次方程代數解
五次方程代數解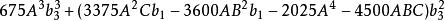 五次方程代數解
五次方程代數解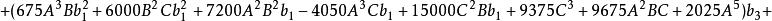 五次方程代數解
五次方程代數解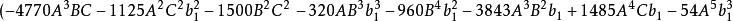 五次方程代數解
五次方程代數解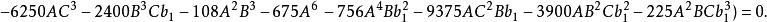 五次方程代數解
五次方程代數解若以函式的觀點來看,方程
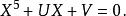 五次方程代數解
五次方程代數解 五次方程代數解
五次方程代數解 五次方程代數解
五次方程代數解的解有兩個自變數, 和 。
若再令
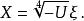 五次方程代數解
五次方程代數解則方程式可以進一步化簡為如下形式:
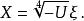 五次方程代數解
五次方程代數解 五次方程代數解
五次方程代數解 五次方程代數解
五次方程代數解它的解 是單一變數 的函式 。
特殊五次方程的求根公式
雖然一般的五次方程不存在根式解,但是對於某些特殊的五次方程,滿足某些條件後還是有根式解的 。
型式2
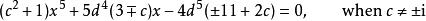 五次方程代數解
五次方程代數解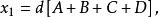 五次方程代數解
五次方程代數解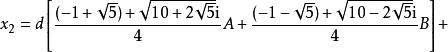 五次方程代數解
五次方程代數解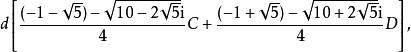 五次方程代數解
五次方程代數解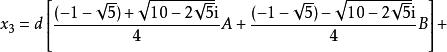 五次方程代數解
五次方程代數解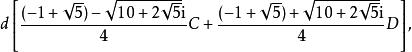 五次方程代數解
五次方程代數解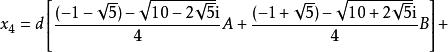 五次方程代數解
五次方程代數解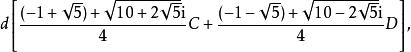 五次方程代數解
五次方程代數解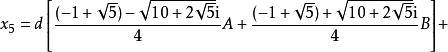 五次方程代數解
五次方程代數解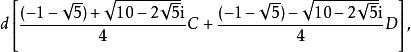 五次方程代數解
五次方程代數解其中
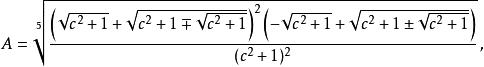 五次方程代數解
五次方程代數解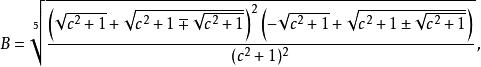 五次方程代數解
五次方程代數解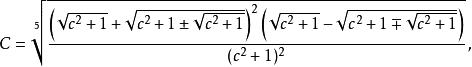 五次方程代數解
五次方程代數解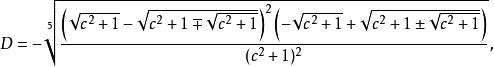 五次方程代數解
五次方程代數解型式3
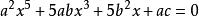 五次方程代數解
五次方程代數解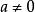 五次方程代數解
五次方程代數解,當時,
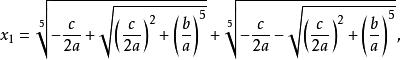 五次方程代數解
五次方程代數解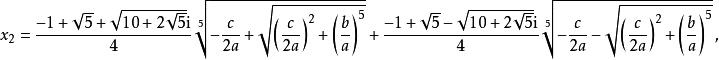 五次方程代數解
五次方程代數解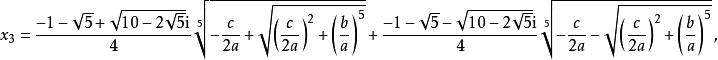 五次方程代數解
五次方程代數解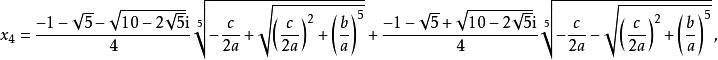 五次方程代數解
五次方程代數解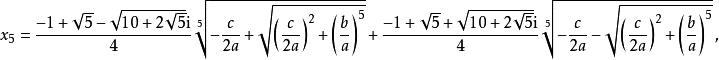 五次方程代數解
五次方程代數解