正約數
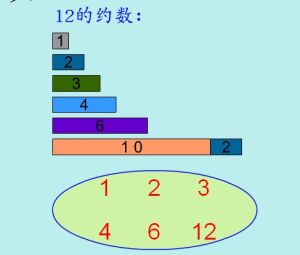
約數：如果一個整數a能把兩個整數b和c整除，那么這兩個數b和c就是這個數a的約數。約數是有限的，一般用最大公約數。所有數都有約數1。正約數是約數中的正數。例：15能被3整除，我們就說15是3的倍數，3是15的約數。
基本信息
正約數
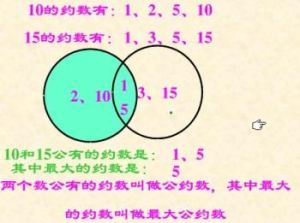約數約數：如果一個整數能被兩個整數整除，那么這兩個數就是這個數的約數。約數是有限的，一般用最大公約數。所有數都有約數1。
例：15能被3整除，我們就說15是3的倍數，3是15的約數。
正約數表示正的約數
如果是求所有公約數，那么還是用15舉例：15首先能被1整除，及1、15。再考慮2，顯然不行，隨後考慮3，發現能整除，4也顯然不行，以此類推。最後所有公約數就是1、3、5、15。
個數定理
正約數對於一個大於1正整數n可以分解質因數：n=p1^a1*p2^a2*p3^a3*…*pk^ak,則n的正約數的個數就是（a1+1）（a2+1）（a3+1）…(ak+1).其中p1，p2，p3…pk都是n的質因數;a1、a2、a3…ak是p1、p2、p3…pk的指數。
定理證明
首先同上，n可以分解質因數：n=p1^a1*p2^a2*p3^a3*…*pk^ak,由約數定義可知p1^a1的約數有:p1^0,p1^1,p1^2......p1^a1，共（a1+1）個;同理p2^a2的約數有（a2+1）個......pk^ak的約數有（ak+1）個。故根據乘法原理：n的約數的個數就是(a1+1）（a2+1）（a3+1）…(ak+1)。
例題
例題：正整數378000共有多少個正約數？解：將378000分解質因數378000=2^4×3^3×5^3×7^1由約數個數定理可知378000共有正約數(4+1)×(3+1)×(3+1)×(1+1)=160個。
