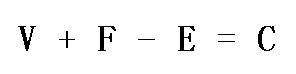 head
head引文:
嵌入 (embedding)
將圖G "嵌入" 一個平面後得到的它在該平面的一個 "嵌入" W, 則:W上的頂點一一對應G上邊的端點, W中的邊一一對應G上的簡單弧, 並滿足:
1.W中任意一條弧的端點對應G中一條邊的頂點.
2.W中任意一條弧上的點和G中頂點不相關
3.W中任意兩條弧的交點對應G中邊的頂點.
簡單弧 (simple arc)
平面內無環路連續曲線.
圖的對偶(dual graph)
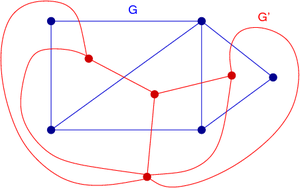
G*是圖G的"對偶" , 則: 在平面內被圖分隔開的每一個區域中取一個點, 並將這些相臨區域中取得的點用邊相連, 得到的圖是G*.
( 對偶的性質是對稱的, 用 "G*" 表示G的對偶,則G** = G)
如圖: G' 與G 互相對偶.
 g
g連通圖 (connected graph)
如果無向圖所有頂點互相可達, 則它是連通的.
生成樹 (spanning tree)
一棵遍歷圖所有頂點的樹.
翻譯的歐拉公式 V + F - E = 2 的19種證明方法
(原文: Nineteen Proofs of Euler's Formula )
"我"的話:
1. 若論思想性、精簡、嚴密, 原文遠勝。 所以贅述, 乃體諒中文資料難求之苦。
2. 歡迎修改
注:
1> 帶引號的詞語, 我也不確定.
2> 斜體詞語, 後面有解釋,
3> 未完成
注2:
1> V + F - E = 2 是拓補學重要公式 (原型被推廣到了凹多面體 V + F - E = C ): . 歐拉公式還有很多
2> 以下證明, 有三個重要的數學模型被使用, 證明中我給出了簡述, 其實不嚴密. 有興趣可以再查資料.
它們是: Jordan curve theorem, dual graph, graph embedding
"結合2棵生成樹"原理:
對於任二維平面內 "嵌入" 的連通圖G, 它的一個"對偶" 是G*.(取G中每個面的中點, 以及G外一點, 相臨面各連一邊成為G的 "對偶": 圖G*)
我們假定: G*中由G相臨面連成的邊, 只被G中這兩個面交線分隔. 那么:
1. G中的環,一定切斷G*
2. G中的樹,一定不會切斷G*
(上面兩個性質的證明用到拓補學的一個定理, Jordan curvetheorem: 這個定理對我們來說是沒什麼疑問, 簡述其旨如下:
一條簡單封閉曲線分平面為兩部分.
但據說這個定理在數學史上的證明大費周折)
證明:
取G的生成樹T, 則T不含環, 且T中邊相對於G的補集 T'同樣不含環 .
因為 T' 沒有切斷 G*, 所以 T' 的對偶仍是生成樹. T的邊數是 (V-1) , (T')* 的 邊數與 T' 相同, 是 (F - 1)
可以證明: 這兩棵生成樹邊數的和是G的邊數: (V- 1) +(F - 1) = E
"簡單歸納"
注: 作者聲明自己不喜歡這樣的證明.
"It is to my mind unnecessarilycomplicatedand inelegant;"
證明1: (歸納面)
將一個圖先 "嵌入" 二維平面得到圖G.
當G只有一個面時 : E(1) = V(1) - 1 + F(1) - 1
當G有N個面時,
設: E(N) =V(N-1) - 1 +F(N-1) - 1
我們去除一條G中兩個面的一條臨邊, 得到G有 N-1個面時
E(N-1) = E(N)- 1
V(N-1) = V(N)
F(N-1) = F(N)
故: E(N-1) =V(N-1) - 1 + F(N-1) - 1
叢而歸納出歐拉公式成立
證明2: (歸納頂點)
將一個圖先 "嵌入" 二維平面得到圖G.
當G只有一個頂點時 (一個簡單環 )
F(1) + V(1) - E(1) = (E(1) + 1) + 1 - E(1) = 2
當G有N個頂點時, 假設結論成立
我們去除一條G中兩個面的一條臨邊, 得到G有 N-1個面時 ,面和邊各減少1. 故結論成立
證明3: (歸納邊)
和上面的方法一個思路
略.
"縮小面的歸納"
證明:
當凸多面體只有一個面時, V(1) + (F(1) - 1) - (E(1) - 1) = 0 顯然成立.
假設當有N個面時這一性貭仍然成立. 這時我們,從凸多面體上取下一個面. 這時多面體成為了一個 "開口的容器".
我們這時在不影響面數的前提下縮小這個 "開口", 直到為一個點.於是得到一個新的凸多面體.
設這個凸多面體比原來少了 M 個頂點, 則這M個頂點在 "開口" 上,因此這個多面體比之原先, 又減少了M條邊.
這樣假設在N - 1 時成立
"電中性"
證明:
 4
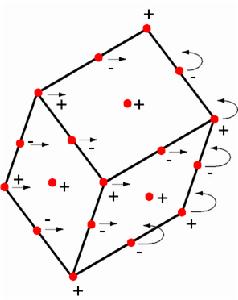
4用一種方法放置, 使圖的邊都不在水平面上, 這樣就產生了最高點U, 最低點L. 在凸多面體的頂點放正單位電荷, 邊中點放負單位電荷, 面中點放正單位電荷.
以下證明, 可以中和除了U, L所在位置外的電荷: 從上往下看, 我們讓所有電荷在水平面 "逆時針" 運動一次到相臨面, 那么:
1> U, L 不動 2> 不考慮U, L, 進入一個面的電荷是該面邊數 e的一半減一. ( e / 2 - 1), 負電荷多一 , 其他電荷除了面中點的一個正電荷全部移出.
故除U,L 完全中和.
得證
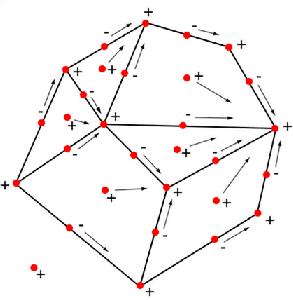
“ 用‘嵌入’ 法中和”
 7
7