簡介
定義
橫截性條件是當容許函式在固定邊界滿足一定的約束的情形時,由變分為零導出的極值函式在邊界上滿足的條件。
具體內容
變分積分
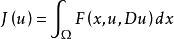 橫截性條件
橫截性條件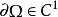 橫截性條件
橫截性條件的積分區域Ω是R 中的有界區域,,u滿足邊界條件
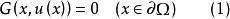 橫截性條件
橫截性條件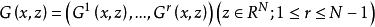 橫截性條件
橫截性條件 橫截性條件
橫截性條件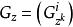 橫截性條件
橫截性條件其中,設 G 在 上屬C ,在集
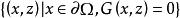 橫截性條件
橫截性條件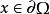 橫截性條件
橫截性條件的每點秩為 r ,對每一,集合
 橫截性條件
橫截性條件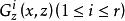 橫截性條件
橫截性條件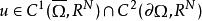 橫截性條件
橫截性條件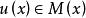 橫截性條件
橫截性條件是 R 中的(N-r)維流形,法向量場是。若 是泛函 J 在邊界約束(1)(即)下的平穩函式,則 u 滿足邊界條件
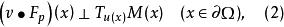 橫截性條件
橫截性條件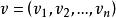 橫截性條件
橫截性條件其中是Ω的單位外法向, F 的分量是
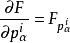 橫截性條件
橫截性條件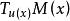 橫截性條件
橫截性條件表示 M(x) 在 u(x) 的切空間,條件 (2)表明在Ω 上的分量為
 橫截性條件
橫截性條件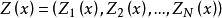 橫截性條件
橫截性條件的向量正交於流行 M(x) 條件 (2) 稱為橫截性條件。
實例
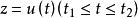 橫截性條件
橫截性條件例如,設 J(u) 是某路徑 的加權距離,則
 橫截性條件
橫截性條件權ω(z)>0 並且是 C (R ) 類的。此時橫截性條件(2)等價於正交條件,即連結 R 中一固定點 P 和 R 中某流形 M 上的某點的最短路徑必和 M 交成直角。
