簡介
在數學中,橫截相交是描述空間如何相交的概念,並在一般的立場上發揮作用。 它形成了差分拓撲中通用交集法。 通過考慮交點處的交叉空間的線性化來定義。
定義
給定有限維平滑多面體的兩個子流形橫截相交,它們在每個相交點處產生多面體的切線空間。不相交的多面體是橫截的。如果多面體具有互補尺寸(即它們的尺寸加在環繞空間的尺寸上),則該條件意味著環繞空間的切線空間是兩個較小切線空間的直接和。如果交叉點是橫截的,則交叉點將是一個子流形,同時等於兩個多面體之和。在沒有橫截條件的情況下,交點可能不會成為子流形,而是某種奇異點。
特別地,這意味著互補的橫截子流形在分離點相交。如果兩個多面體和環繞空間都是定向的,那么它們的交叉是面向的。當交叉點為零時,每個點的方向只是簡單的加或減。
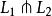 橫截相交
橫截相交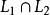 橫截相交
橫截相交給定多面體M的兩個子流形L和L的橫截交叉點的一個符號是。 這種符號可以用兩種方式讀取:或者作為“L和L橫截相交”,或者當該交點橫向時,作為L和L的集合論裡面的交集的替代符號。 在這個符號中,橫截相交的定義讀作
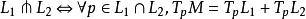 橫截相交
橫截相交地圖的橫截性
一對子流形的橫截性的概念很容易擴展到子流體的橫向和地圖到環繞流形,或一對映射到環繞多面體,這是通過沿著圖像的相交點的切線空間的推動是否產生環繞流形管的整個切線空間。如果地圖是嵌入式的,這等價於子流體的橫截性。
不同維度橫截的意義
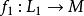 橫截相交
橫截相交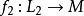 橫截相交
橫截相交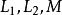 橫截相交
橫截相交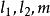 橫截相交
橫截相交假設我們有橫截圖和其中是具有維度分別為的流形。
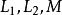 橫截相交
橫截相交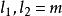 橫截相交
橫截相交根據的相對維度,橫截的含義有很大的不同。 當時橫截和相切之間的關係是最明顯的。
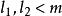 橫截相交
橫截相交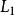 橫截相交
橫截相交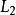 橫截相交
橫截相交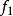 橫截相交
橫截相交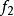 橫截相交
橫截相交當時,和的任意點跨越M的切線空間。 因此,和之間的任何交集都不能橫截。 然而,不相交的多面體真空滿足條件,因此可以說橫截相交。
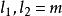 橫截相交
橫截相交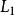 橫截相交
橫截相交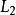 橫截相交
橫截相交當時,和的切線空間必須直接與任意交點處的M的切線空間相加。 它們的交集因此由分離的有符號點組成,即零維流形。
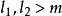 橫截相交
橫截相交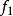 橫截相交
橫截相交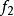 橫截相交
橫截相交當這個總和不一定是直接的。 事實上,如果和在其交點處侵入,這是不直接的,就像嵌入式子流程的情況一樣。
相交產物
給定任何兩個平滑子流形,可以通過任意小的量來擾亂其中任一個,使得所得到的子流體與固定子流形橫截相交。 這種擾動不影響多面體或其交點的同源性。 例如,如果互補尺寸的多面體橫截相交,即使我們將多面體同位於另一個橫截交叉點,其交點數也不會改變。
橫截相交的例子
橫向的最簡單的例子是弧。 若且唯若它不是切線,即它們在與表面相切的平面內的切線不同時,兩個弧之間的交點是橫向的。
在三維空間中,橫向曲線不相交。 橫向於曲面的曲線以點相交,並且彼此橫向的表面在曲線中相交。 在某一點(例如,位於表面上的曲線)上與曲面相切的曲線不橫向交叉。
套用
最佳控制
在利用微積分變化或相關龐特里亞金最大原理的領域中,橫向條件經常用於控制最佳化問題中找到的解決方案的類型。 例如,解決曲線是形式問題的必要條件:
最小化
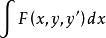 橫截相交
橫截相交其中一個或兩個端點,曲線不固定。
在許多這些問題中,解滿足條件是解曲線應橫向跨越零線或描述終條件的其他曲線。
解空間的平滑度
使用薩德定理,其假設是地圖的橫向的特殊情況,可以顯示互補尺寸空間或子流形之間的子流體和映射到空間之間的橫向交點本身是平滑的子流形。例如,如果定向多面體的切線束的平滑部分矢量場 - 被視為從基地到總空間的地圖,並且橫截面與零段(被看作地圖或子集合)相交,然後與該區段的零集相交。矢量場的奇異點形成基底的平滑0維子流形,即一組符號點。符號符合矢量場的指標,因此符號的總和即 - 零集合的基本類別等於多面體的歐拉特徵。
一個非常特殊的情況如下:如果從實數到實數的可微函式在函式的零點上具有非零導數,那么該圖在該零點處橫向於x軸;零微分將意味著曲線的水平切線,這將與x軸的切線空間一致。
對於無限維的例子,d-bar運算符是從黎曼表面到幾乎複雜的流形的映射空間上的某個巴拿赫空間束的一部分。本節的零集由全息圖組成。如果顯示d-bar操作符與零段橫向,則該模量空間將是一個平滑的多面體。這些考慮在假變形曲線和格羅莫夫 - 威滕理論的理論中起著重要的作用。
