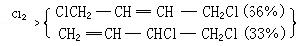模糊關係
正文
論域（直積空間）X×Y＝{(x，y)│x∈X，y∈Y}中的模糊關係垾就是X×Y中的模糊集垾的隸屬函式
在實軸閉區間【0，1】上取值,的大小反映元素x與y之間的關聯程度。一般，X＝X1×X2×…×Xn中的n項模糊關係,是X1×X2×…×Xn中的模糊集垾,它的隸屬函式用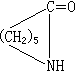
表示,xi∈Xi，i＝1,2，…,n。模糊關係是普通關係的拓廣。普通關係描述事物之間是否有關聯，而模糊關係則描述事物之間關聯程度的多少。L.A.扎德將模糊關係套用於輸入、輸出和狀態間有模糊關係的模糊系統中。模糊關係還套用於有限自動機、算法、語言學等方面。 模糊矩陣和模糊關係圖 設X＝{ x1, x2，…， xm}和Y＝{ y1，y2，…, yn}是有限論域，則X，Y 的模糊關係垾可用n×m 矩陣R 表示：
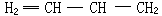矩陣R稱為模糊關係垾的模糊矩陣。模糊矩陣還可以用相應的圖來表示，稱為模糊關係圖（見圖）。 
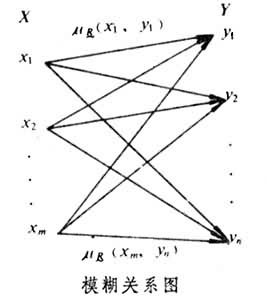模糊關係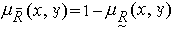
，則稱捪是垾的補集。 兩個模糊關係垾1與垾2的並垾1∪垾2,是指對任何的(x，y)∈X×Y都有
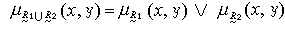，其中“a∨b”表示在ɑ，b中取較大者。 兩個模糊關係垾1與垾2的交 垾1∩垾2, 是指對任何的(x，y)∈X×Y 都有
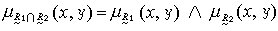，其中“a∧b”表示在ɑ，b中取較小者。 兩個模糊關係垾與垾-1，如果對任何的(x，y)∈X×Y，都有
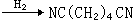，則稱 垾-1是垾的逆轉關係，又稱倒置關係。 模糊關係嫢稱為恆等關係，是指若且唯若對任何的(x，y)∈X×Y，都有
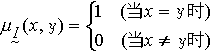
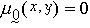。 模糊關係啇 稱為全稱關係，是指若且唯若對任何的(x，y)∈X×Y，都有
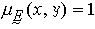。 X×Y上的模糊關係垾與Y×Z上的模糊關係慒 的合成，記作垾⋅慒,是指對任何的(x,z)∈X×Z,都有
＝
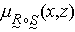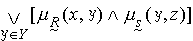,式中,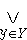
,表示對所有y ∈Y求【 】中的最大值,∧表示求其前後兩項中的最小值。 X×X上的二元模糊關係 垾具有自反性、對稱性、反對稱性和傳遞性。
自反性是指對任何的x∈X，都有
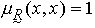。 對稱性是指對任何的(x，y)∈X×X，都有
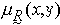
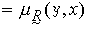。 反對稱性是指對任何的(x，y)∈X×X，
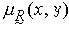
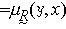的充分必要條件是
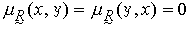。 傳遞性是指對任何的(x，y),(y，z),(x，z)∈X×X，都有
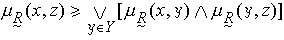。 模糊相似關係和模糊等價關係 若X×X上的模糊關係 垾滿足自反性與對稱性，則稱垾為X的一個模糊相似關係，又稱模糊相容關係。
表示x與y對於模糊關係垾的相似程度。當X為有限集時,模糊相似關係可用一個主對角線元素為1的對稱模糊矩陣來表示。若X×X上的模糊關係 垾滿足自反性、對稱性和傳遞性，則稱垾為X的一個模糊等價關係。模糊相似關係和模糊等價關係是模糊聚類分析和模糊綜合評判的基本數學工具。 模糊關係方程 在模式識別、綜合評判等方面經常遇到模糊關係方程的問題。如果已知模糊關係捜和慒，要求解出滿足捜⋅垾＝慒的模糊關係垾，這時捜⋅垾＝慒就是一個模糊關係方程。
