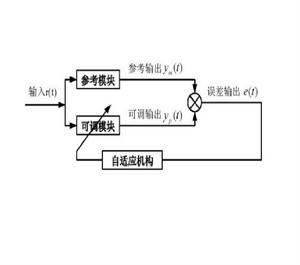
基本概念
模型跟隨自適應控制(AMFC)是一種基於超穩定性理論，針對參數未知(時變)線性系統的模型跟隨控制方法。這種方法穩定性容易保證，系統設計也較方便，且具有較好的抗擾變性和控制精度。
工程實踐中，有些機電系統，其工況不允許線上辨識，驗前知識甚少，還要求高性能，現有控制方法難以奏效，是當前工程學術界研究的課題。模型跟隨自適應拉制(AMFC)是MRAC的一個分支，AMFC的核心是線性模型跟隨控制(LMFC)和波波夫超穩定性理論，LMFC由於滿足模型完全可跟隨(PMF)條件，以能獲得高精度而具有吸引力，近年國外還在探索套用。
PMF條件
PMF條件可以歸結為兩個矩陣M和N的乘積為零，一般地，M和N均可視為n維內積空間V中的兩個矢量集，因為：
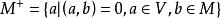模型跟隨自適應控制
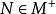模型跟隨自適應控制要求MN=0，即 。
控制方法
最小範數狀態法
參考模型：
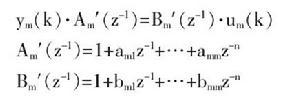模型跟隨自適應控制已知SISO系統：
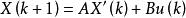模型跟隨自適應控制
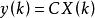模型跟隨自適應控制
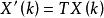模型跟隨自適應控制對於任意n維正交陣T，有 。
當系統參數未知時，(A、B、C)、(A'、B、C')和T均未知，選定C'，對應於一定的最小實現(A'、B'、C')和特定的正交陣，以及代數等價系統(A、B、C)。這樣，在控制中求取最小範數狀態作為滿足PMF條件的狀態重構時，對輸出陣的選擇可以有極大的主觀隨意性。
直接狀態法
以輸出直接作為狀態，不需重構狀態，稱之為直接狀態法。當輸入陣只有一個非零元素時，PMF條件自動滿足，由控制理論可知，當傳遞函式只在原點有零點，以狀態空間表達式實現時，其輸入陣和輸出陣都只有一個非零元素，就可以輸出作為狀態且自動滿足PMF條件。
綜前所述，AMFC方法有兩個基本點：一是滿足波波夫超穩定理論的兩個條件，即前向傳遞函式嚴正實，反饋通道滿足波波夫不等式；二是滿足PMF條件。
套用
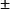模型跟隨自適應控制從1985年研究AMFC新方法以來，首先套用在千噸級雙通道禍合高精度同步電液載入系統的解耦控制。50年代以來，國內大量生產的WE型材料試驗機，原設計只進行簡單拉壓試驗，採用柱塞缸液壓系統。為改造它以增加疲勞試驗，分析了它的動特性，採用AMFC新方法，使其在各種試驗條件下獲得了 1%的高精度。
模型跟隨自適應控制(AMFC)是一種基於超穩定性理論，針對參數未知(時變)線性系統的模型跟隨控制方法。這種方法穩定性容易保證，系統設計也較方便，且具有較好的抗擾變性和控制精度。電液伺服系統線性化處理後，可套用AMFC，在一定條件下也可取得較好的控制效果，如果將AMFC直接用於電液伺服非線性系統，則可能成為一種極具潛力的控制方法。模型跟隨自適應控制可直接用於電液伺服非線性系統，且其模型完全可跟隨條件也能自動滿足。但這種方法需要利用位移、速度和加速度或壓力信號，這也是對系統進行非線性補償所付出的代價，如何降低這種代價是有待進一步研究的問題。
