基本介紹
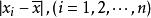絕對離差
絕對離差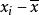絕對離差是指各個觀測值與均值相減的絕對值，通常表示為，在計算平均差、標準差等時也會用到，可以表示數據分布的集中程度，其中稱為離差。
離差
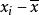絕對離差離差即標誌變動度，又稱“偏差”，是觀測值或估計量的平均值與真實值之間的差，是反映數據分布離散程度的量度之一，或說是反映統計總體中各單位標誌值差別大小的程度或離差情況的指標，常寫作，即參與計算平均數的變數值與平均數之差。離差的性質有二： (1)離差的代數和等於0；(2)參與計算平均數的各變數值與平均數之差的平均和，小於這些變數值與平均數之外的任何數之差的平均和。由於這兩種性質，使離差在描述統計中運用較廣。
在統計中用來測定標誌變動度的指標主要有：平均差、標準差、全距、四分位差、十分位差和離散係數等，離差是測定樣本代表性的重要指標，例如我們在選擇時，有兩組工人，每組都是5人，第一組每人日產分別為10，23，45，52，60，平均每人日產38件；第二組每人日產分別為35，39，42，39，38，平均每人日產也是38件，但我們可以看出，第二組的樣本較第一組樣本更加接近平均數，因此，第二組代表也較第一組強，從這裡可以看出，標誌變動度越小，樣本的代表性較強，反之，則樣本的代表性越強。
計算公式
簡介
平均差也稱平均絕對離差，是各個觀測值與均值的絕對離差之和除以觀測值的個數，也可以說是總體各單位標誌值與其算術平均數的離差絕對值的平均數。加絕對值是為了避免正負離差相互抵消總和為零。
平均差的計算
簡單平均差的計算公式
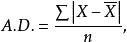絕對離差
絕對離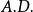差
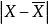絕對離差
絕對離差式中，為 平均差；X為標誌值；為算術平均數；為 絕對離差；n為項數 。
加權平均差的計算公式
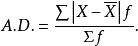絕對離差平均絕對離差的主要特徵：
a. 它不會受到極端大的或極端小的數值的影響；
b. 它的計算利用了全部觀測值；
c.絕對值處理起來有些困難。
平均差的作用：
(1)平均差計算簡便，意義明確。
(2)平均差能將總體中所有各單位的標誌值的差異情況全部包括進去，較準確地反映了總體各單位標誌值的離差程度。
平均差的局限性：
(1)運算絕對值雖然可解決離差正負抵消的問題，但不適合代數方法的演算。
(2)用算術平均數計算的絕對離差之和不是最小。如果用中位數代替算術平均數則更加妥當 。
