定義
 函式圖
函式圖 極值點
極值點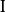 極值點
極值點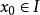 極值點
極值點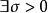 極值點
極值點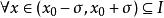 極值點
極值點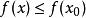 極值點
極值點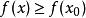 極值點
極值點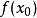 極值點
極值點 極值點
極值點 極值點
極值點 極值點
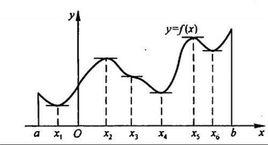
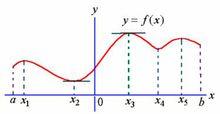
極值點設函式在區間有定義,,若, 有 (或),則稱是函式的一個極大值(或極小值), 是函式的一個極大值點(或極小值點)。極大值與極小值統稱為極值;極大值點與極小值點統稱為極值點。上面的不等號若嚴格成立,則稱為嚴格極值點,對應函式值稱為嚴格極值。
注意:
 極值點
極值點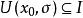 極值點
極值點 極值點
極值點 極值點
極值點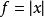 極值點
極值點 極值點
極值點(1)極值點只關心在 內的局部函式值,不關心是否可導。因此函式在極值點處可能不可導,如 在 處不可導。
(2)極值點是函式圖像的某段子區間內上極大值或者極小值點的橫坐標。
(3)極值點出現在函式的駐點(導數為0的點)或不可導點處(導函式不存在,也可以取得極值,此時駐點不存在)。
 極值點
極值點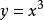 極值點
極值點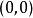 極值點
極值點(4)可導函式的極值點必定是它的駐點。但是反過來,函式的駐點卻不一定是極值點,例如,點是它的駐點,卻不是它的極值點。
 極值點
極值點(5)極值點上的導數為零或不存在,且函式的單調性必然變化。
定理
 極值點
極值點 極值點
極值點 極值點
極值點 極值點
極值點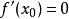 極值點
極值點若函式在處可導,且是函式的極值點,則
 極值點
極值點 極值點
極值點 極值點
極值點 極值點
極值點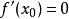 極值點
極值點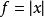 極值點
極值點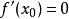 極值點
極值點 極值點
極值點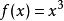 極值點
極值點 極值點
極值點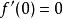 極值點
極值點 極值點
極值點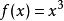 極值點
極值點註:若去掉“函式在處可導”的條件,則函式的極值點處不一定有,如;此外,若,則不一定是極值點,如在處,有,但不是的極值點。
判別方法
 極值點
極值點(1)若函式可導
 極值點
極值點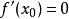 極值點
極值點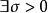 極值點
極值點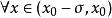 極值點
極值點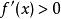 極值點
極值點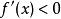 極值點
極值點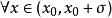 極值點
極值點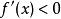 極值點
極值點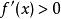 極值點
極值點 極值點
極值點 極值點
極值點【第一判別法】若函式可導,,且,有(或)同時,有(或),則是函式的極大點(或極小點)
 極值點
極值點 極值點
極值點 極值點
極值點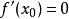 極值點
極值點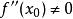 極值點
極值點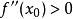 極值點
極值點 極值點
極值點 極值點
極值點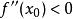 極值點
極值點 極值點
極值點 極值點
極值點【第二判別法】若函式存在二階導數,是函式的穩定點,即,而,則當時,是函式的極小點;當時,是函式的極大點。
 極值點
極值點(2)若函式在一些點不可導,則需要用定義判斷。
計算方法
(1)單變數函式的極值求法
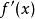 極值點
極值點a. 求導數;
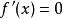 極值點
極值點b. 求方程的根;
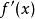 極值點
極值點 極值點
極值點 極值點
極值點c. 檢查在函式圖象左右的值的符號,如果左正右負,那么在這個根處取得極大值;如果左負右正,那么在這個根處取得極小值。
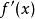 極值點
極值點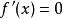 極值點
極值點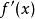 極值點
極值點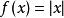 極值點
極值點 極值點
極值點特別注意:無意義的點也要討論,即可先求出的根和無意義的點,這些點都稱為可疑點,再用定義去判斷。 例如: 在的導數是不存在的。
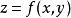 極值點
極值點(2)二階連續偏導數的函式的極值求法,敘述如下:
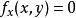 極值點
極值點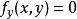 極值點
極值點a. 解方程組,,求得一切實數解,即可求得一切駐點;
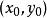 極值點
極值點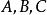 極值點
極值點b. 對於每一個駐點,求出二階偏導數的值;
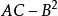 極值點
極值點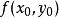 極值點
極值點c. 定出的符號,判定是否是極值,是極大值還是極小值。
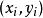 極值點
極值點注意:當函式僅在區域D內的某些孤立點不可導時,這些點不是函式的駐點,但這種點有可能是函式的極值點,要注意另行討論。
極值點與穩定點
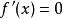 極值點
極值點 極值點
極值點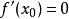 極值點
極值點 極值點
極值點方程的解,即稱為函式的穩定點
 極值點
極值點 極值點
極值點註:定義不要求函式可導,所以可導函式的極值點必須是穩定點,但穩定點不一定是極值點。