基本概念
約束極值 約束極值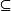約束極值亦稱條件極值，約束極值問題的典型形式是：已知g：E(R )→R，g(x)=0，x∈DE (i=1，2，…，m;1≤m<n)，求函式f：E→R的極值，即求函式f(x)限制在集合：
D={x∈E|g(x)=0，i=1，2，…，m}
上的極值，這個極值就稱為f(x)的滿足條件g(x)=0(i=1，2，…，m)的約束極值。這樣，f(x)在a∈D達到約束極小(極大)值，意味著存在開球B(a，r)，使x∈D∩B(a，r)時，f(x)≥f(a)(f(x)≤f(a))，f稱為目標函式，g(x)=0(i=1，2，…，m)稱為約束條件。相對而言，f(x)在其定義域E上的(絕對、局部)極值稱為無約束極值或自由極值 。
解約束極值問題的基本方法
基本介紹
解約束極值問題的基本方法是把它化為新目標函式的無約束極值問題。這有兩條途徑：一是設法取消約束條件，例如從所給的m個約束條件中解出m個自變數，設為x=φ(x，x，…，x)，i=1，2，…，m，把目標函式變成n-m元函式φ(x，x，…，x)=f(φ(x，x，…，x)，…，φ(x，x，…，x)，x，…，x)，然後求φ的無約束極值，這種方法稱為代入法。或以其他參數表示x(j=1，2，…，n)，設為x=ψ(t，t，…，t)(k<n)，把f(x)變成k元函式ψ(t，t，…，t)=f(ψ(t，t，…，t)，…，ψ(t，t，…，t))，然後求ψ的(無約束)極值。另一途徑是不取消約束條件，把它與目標函式一起考慮，建立適當的新目標函式。這方面一種最常用的方法是拉格朗日乘數法。除了上述等式形式的約束條件外，還可以用不等式給出約束條件：
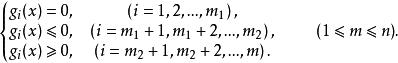約束極值若所有g(x)與目標函式都是線性函式，則相應的約束極值問題稱為線性規劃問題，否則稱為非線性規劃問題，這些問題在最最佳化理論中研究 。
拉格朗日乘數法
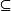約束極值拉格朗日乘數法是求約束極值的一種方法，其基本思想是引進參數，把約束極值問題化為無約束極值問題。設需要求目標函式f：E(R )→R在約束條件g(x)=0(g：E→R，i=1，2，…，m，m<n)下的極值，拉格朗日乘數法是：若E是開集，f，g(i=1，2，…，m)都是C 類的，D={x∈E|g(x)=0，i=1，2，…，m}，矩陣(Dg(a))(即向量函式g=(g，g，…，g)的雅可比矩陣g′(a))的秩是m，則f在a∈D達到約束極值的必要條件是存在常數λº，λº，…，λº，使：
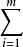約束極值Df(a)+λºDg(a)=0，(j=1，2，…，n)，
即Df(a)+λºDg(a)+…+λºDg(a)=0。這樣就把f的約束極值問題化為函式：
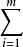約束極值F(x;λ)=f(x)+λg(x)
的無約束極值問題 。這個函式稱為拉格朗日函式，λ，λ，…，λ稱為拉格朗日乘數.拉格朗日函式是(x，λ)=(x，x，…，x，λ，λ，…，λ)的n+m元函式.它的駐點加上使f，g，g，…，g之一不連續或不可微的點及使得矩陣(Dg(x))的秩小於m的點，就是所有可能達到條件極值的點.當這樣的點惟一時，往往可以從具體問題的背景判斷其為極大或極小.當有若干個這樣的點時，除通常用拉格朗日函式的黑塞矩陣判定外，還可用其他方法判定.下面是其中的一個充分條件：設f，g，g，…，g都是C 類的，(x，λ)是拉格朗日函式的駐點，若對滿足：
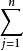約束極值Dg(x)h=0 (i=1，2，…，m)
的h=(h，h，…，h)≠0(x+h∈D∩B(x，r))均有：
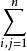約束極值DF(x，λ)hh>0(<0)，
則f(x)在x處達到條件極小(極大)值。在約束條件包含不等式的情形，也可寫出適當的拉格朗日函式並得到類似的必要條件，這在規劃論中研究 。
