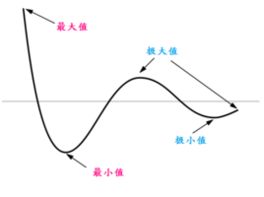
基本介紹
一個函式的極大值或極小值。如果一個函式在一點的一個鄰域內處處都有確定的值,而以該點處的值為最大(小),這函式在該點處的值就是一個極大(小)值。如果它比鄰域內其他各點處的函式值都大(小),它就是一個嚴格極大(小)。該點就相應地稱為一個極值點或嚴格極值點。
分類介紹
extremum
數學函式的一種穩定值,即一個極大值或一個極小值,極值點只能在函式不可導的點或導數為零的點中取數學中的極值計算示例圖
得。
extremevalue
在給定的時期內,或該時期的一定月份或季節內觀測到的氣候要素的最高值或最低值。如果這個時期是整個有觀測資料的時期,這個極值就是絕對極值
相關定義
 星空極值
星空極值極值的概念來自數學套用中的最大最小值問題。定義在一個有界閉區域上的每一個連續函式都必定達到它的最大值和最小值,問題在於要確定它在哪些點處達到最大值或最小值。如果不是邊界點就一定是內點,因而是極值點。這裡的首要任務是求得一個內點成為一個極值點的必要條件。
設函式f(x)在x。附近有定義,如果對x。附近的所有的點,都有f(x)f(x。),則f(x。)是函式f(x)的一個極小值,極大值與極小值統稱為極值。
多變數函式
對於多變數函式,同樣存在在極值點的概念,但是也有 鞍點的概念。
舉例
例題
求函式f(x,y)=x^3+y^3-2x^2-2y^2+6x的極值
應該是fx=0,fy=0得到四個點,再代入值比較大小。
fx=3x^2-4x+6>0恆成立
fy=3y^2-4y=0得到y=0或者y=4/3
定理1(必要條件): 設函式z = f(x,y)在點(x0,y0)具有偏導數,且在點(x0,y0)處有極值,則它在該點的偏導數必然為零
fx(x0,y0) = 0,fy(x0,y0) = 0。
定理2(充分條件): 設函式z = f(x,y)在點(x0,y0)的某領域內連續且有一階及二階連續偏導數,又fx(x0,y0) = 0,fy(x0,y0) = 0,令
fxx(x0,y0) = A,fxy(x0,y0) = B,fyy(x0,y0) = C,
則f(x,y)在(x0,y0)處是否取得極值的條件如下:
(1)AC-B2>0時具有極值,且當A<0時有極大值,當A>0時有極小值;
(2)AC-B2<0時沒有極值;
(3)AC-B2=0時可能有極值,也可能沒有極值,還需另作討論。
利用定理1、2,我們把具有二階連續偏導數的函式z = f(x,y)的極值的求法敘述如下:
第一步 解方程組fx(x,y) = 0,fy(x,y) = 0,求得一切實數解,即可求得一切駐點;
第二步 對於每一個駐點(x0,y0),求出二階偏導數的值A、B和C;
第三步 定出AC-B2的符號,按定理2的結論判定f(x0,y0)是否是極值、是極大值還是極小值。
說明
上面介紹的極值必要條件和充分條件都是對函式在極值點可導的情形才有效的。當函式僅在區域D內的某些孤立點(xi, yi)不可導時,這些點當然不是函式的駐點,但這種點有可能是函式的極值點,要注意另行討論。