基本介紹
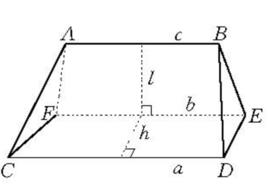
楔體是一種特殊的擬柱體，將一個三稜柱(直三稜柱或斜三稜柱)用一個與三棱相交的截面(直截面或斜截面)去截開，所得的幾何體稱為 楔體。它是一種擬柱體，下底面為梯形或平行四邊形，上底面是與下底面的平行邊平行的線段。圖1中畫出了楔體AB-CDEF。中國古算書《九章算術》中給出了當AE面垂直於CE面時被稱為羨除的體積計算公式為
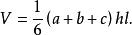楔體
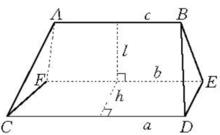圖1楔體與擬柱體
擬柱體 所有頂點都在兩個平行的平面上的多面體叫做擬柱體。它在這兩個平面內的面叫做擬柱體的底面，其餘各面叫做擬柱體的側面，兩底面之間的距離叫做擬柱體的高，通過高的中點且平行於底面的截面叫做擬柱體的中截面(圖2) 。
圖2楔體 擬柱體的兩底都是矩形，並且對應邊平行，這種擬柱體叫做長方台（圖3左）。如果擬柱體的下底面是梯形或平行四邊形，上底面變成了與下底面平行的線段，這樣的擬柱體叫做 楔體（圖3右）。
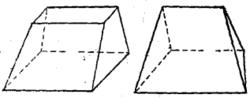圖3擬柱體除有長方台和楔體兩種特殊情形外，從定義可知，還有下面一些特殊情形：
1.如果擬柱體的兩底面是全等的多邊形，並且對應邊平行，則這樣的擬柱體就是稜柱。
2.如果擬柱體的一個底面變為一點，則擬柱體就變為稜錐。
3.如果擬柱體的兩底面是相似多邊形，並且對應邊平行，則這樣的擬柱體就是稜台。
顯然，正四稜台也是長方台的特殊情形，三稜柱也可以看作是楔體的特殊情形 。
擬柱體及楔體的體積公式
現在我們研究擬柱體體積公式一辛普松定理：
定理 任意擬柱體的體積，等於它的高h與上底面積S下底面積S，中截面積S四倍的和的六分之一。即：
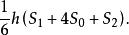楔體V=
【例1】已知楔體下底上平行棱MN、CD的長是a、b，平行於它們的棱KL長為c，垂直於這些棱的直截面面積為S'，求楔體的體積。
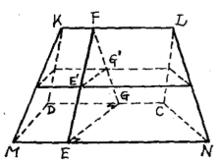圖4解 設楔體的直截面EFG與中截面的交線為E'G'(圖4)因為楔體是擬柱體的特殊情形。
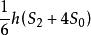楔體所以它的體積 V=
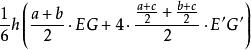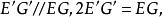楔體
楔體因為
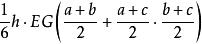楔體所以V=
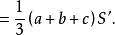楔體