楊-米爾斯理論
正文
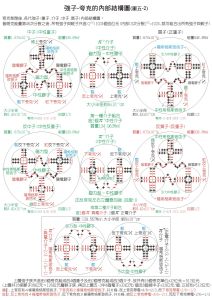 強子(參與強相互作用的基本粒子)的結構模型圖
強子(參與強相互作用的基本粒子)的結構模型圖從物理學知道,電磁場的強度E和H可以用閔科夫斯基時空中的反對稱張量Fλu表示(λ,μ=1,2,3,4):
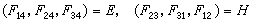 , (1)
, (1)
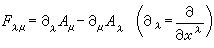 , (2)
, (2)
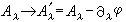 , (3)
, (3)
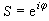 ,
, 那么規範變換就可以用U(1)群的李代數u(1)(i為其基)中的關係式來表示
那么規範變換就可以用U(1)群的李代數u(1)(i為其基)中的關係式來表示 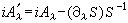 ,
,
楊振寧和R.L.米爾斯根據中子和質子的同位旋對稱性(用群SU(2)來體現),預言必存在某些場,它們由規範勢bλ所定義,bλ∈su(2),(su(2)記SU(2)的李代數),它們也有規範變換
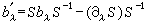 。 (4)
。 (4)
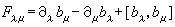 。 (5)
。 (5)
用數學的語言來說,楊-米爾斯的規範勢就是閔科夫斯基空間R 3,1 上的直積纖維叢G×R3,1 上的聯絡,Fλu就是曲率。
然而楊-米爾斯還提出了楊-米爾斯作用量(規範勢的泛函)
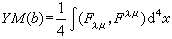 。
。
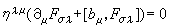 。
。
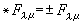
楊-米爾斯場數學問題的研究還有許多方面的問題。中國數學家和理論物理學家對楊-米爾斯場的研究作了若干貢獻。
