歷史及理論描述
在一份私人信件中，沃爾夫岡·泡利在1953年提出了愛因斯坦的廣義相對論的六維理論，將Kaluza、Klein、Fock等五維理論擴展到高維的內部空間。然而，沒有證據表明泡利發展了一個量子場的拉格朗日或它的量子化。因為泡利發現他的理論“導致了一些非物質的陰影粒子”，他沒有正式公布結果。雖然保利沒有發表他的六維理論，但他在蘇黎世發表了兩份關於它的演講。最近的研究表明，擴展的kaluza - klein理論一般不等同於楊斯-米爾斯理論，因為前者包含了額外的術語。
1954年初，楊振寧和羅伯特·米爾斯(Robert Mills)將量子電動力學(量子電動力學)的概念推廣到非阿比利亞群，以解釋強相互作用。楊-米爾斯的觀點受到了保利的批評，因為為了保持標準的不變性，我們必須對楊-米爾斯場的量子位進行無質量控制。這一想法被擱置到1960年，當時，由Jeffrey Goldstone、Yoichiro Nambu和Giovanni jona - lasinio提出，在無質量理論中，通過對稱性破環而獲得質量的粒子概念被提出。
這促使了楊米爾斯理論研究的重新啟動，證明了這兩種理論都成功地套用了電弱統一和量子色動力學(QCD)。電弱相互作用是所描述的SU(2)×U(1)集團在量子色SU(3)楊振寧米爾斯理論。電弱理論由SU(2)與U(1)結合得到，量子電動力學(QED)由U(1)組描述，由表示弱高電荷而非電荷的U(1)組在統一電弱理論中取代。無質量的玻色子的SU(2)×U(1)理論混合後自發對稱性破缺,並產生大量3弱玻色子,光子領域。統一的標準模型結合了強相互作用電弱相互作用(統一弱者和電磁相互作用)通過對稱群SU(2)×U(1)×SU(3)。在目前的時代，強烈的相互作用並不是與電弱相互作用相結合，而是從耦合常數的運行中，相信它們都匯聚到一個非常高的能量的單一值。
在量子色動力學中，能量較低的現象學並沒有被完全理解，因為很難用強耦合來管理這樣的理論。這可能是為什麼禁閉在理論上沒有被證明的原因，儘管它是一個一致的實驗觀察。證明了QCD在低能量範圍內的限制是一個非常重要的數學問題，並由克萊數學研究所提出，無論誰也能證明楊米爾斯理論存在著一個巨大的差距及其存在。
數學定義
楊氏理論是由拉格朗日所給出的非阿貝爾對稱群的一種特殊的量規理論：
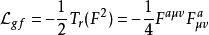楊一米爾斯方程與f量(曲率或場強形式)相對應的李代數的生成器滿足：
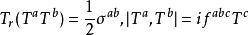楊一米爾斯方程協變導數定義為：
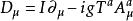楊一米爾斯方程其中，I是群生成器的標識。
該領域具有自相互作用的性質，而得到的運動方程據說是半線性的，因為非線性是同時存在且沒有導數的。這意味著，只能用微擾理論來管理這一理論，有小的非線性。
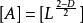楊一米爾斯方程
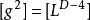楊一米爾斯方程我們在這裡給出一些關於耦合的物理維度的注釋。我們注意到，在D維度，域尺度所以耦合必須等效於。這意味著，對於大於4的維度，楊-米爾斯理論並沒有被重新定義。此外，我們注意到，對於D = 4，耦合是無量綱的，耦合的場和方陣都有相同的場維，以及無質量的夸克標量場理論的耦合。因此，這些理論在經典層面上具有比例不變性。
量化
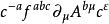楊一米爾斯方程
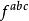楊一米爾斯方程對於量子動力學來說，虛場解耦是因為量規組是阿貝耳曼。這可以從表欄位之間的耦合和鬼域。對於阿貝爾的情況，所有的結構常數是零，所以沒有耦合。在非abelian案例中，幽靈場作為一種有用的方法來重寫量子場理論，而不會對諸如交叉部分或衰變率等理論的可見性產生物理影響。
楊氏理論得到的最重要結果之一是漸近自由。該結果可以通過假設耦合常數g小(小非線性)，高能量和套用攝動理論得到。這一結果的相關性在於，一種描述強相互作用和漸近自由的秧子理論可以適當地處理來自深層非彈性散射的實驗結果。
為了獲得高能量的陽鋼理論的行為，為了證明其漸近自由，一個套用攝動理論假設一個小耦合。這是在紫外線極限下驗證的後驗。在相反的極限情況下，紅外極限，情況則相反，因為耦合太大，擾動理論難以可靠。大多數研究遇到的困難都是在低能量下管理理論。這是一種有趣的情況，是對強子物質的描述，更普遍地，對所有觀察到的膠子和夸克的束縛態和它們的約束。研究這個極限理論的最常用方法是試著在計算機上解決它。在這種情況下，需要大量的計算資源來確定無限體積(小格間距)的正確極限。這是極限，結果必須與。較小的間距和較大的耦合併不相互獨立，而且每個都需要更大的計算資源。從今天開始，對於強子光譜和膠子和幽靈傳播體的計算，情況似乎有些令人滿意，但由於這些奇異的狀態的實驗觀察，膠子和混合譜仍然是一個被質疑的問題。事實上，σ共振中未見任何這樣的格子計算和對比提出了解釋。這是一個備受爭議的問題。
套用
為了理解理論在大、小動量下的行為，一個關鍵的量是傳播器。對於一個秧苗理論，我們必須同時考慮膠子和虛傳播器。在大動量(紫外線極限)下，這個問題完全解決了漸近自由的發現。在這種情況下，可以看出該理論是自由的(對於重整化群來說是微不足道的紫外固定點)，而且膠子和虛傳播器都是自由無質量的粒子。理論的漸近狀態由帶有相互作用的無質量膠子表示。
在低動量(紅外極限)，這個問題更需要解決。其原因是該理論在這種情況下具有很強的耦合性，不能套用攝動理論。唯一可靠的方法是在一台足夠大的計算機上執行格子計算。對這個問題的回答是一個基本的問題，因為它將提供對監禁問題的理解。另一方面，我們不應該忘記，傳播者是一種依賴於度量的量，因此，當一個人想要得到有意義的物理結果時，他們必須謹慎管理。
另一方面，理論方法是為了在這種情況下獲得對理論的理解。先鋒作品是由Vladimir Gribov和Daniel Zwanziger設計的。Gribov發現了一個關於在揚-米爾斯理論中進行測量的問題:他表明，即使一個測量值是固定的，自由也被保留了(Gribov含糊不清)。此外，他還能在朗道量表中為gluon傳播者提供一種功能形式。
這種傳播器不能以這種方式正確，因為它將違反因果關係。另一方面，它提供了線性上升的潛力，這將給夸克約束提供理由。這個函式形式的一個重要方面是，gluon傳播器在動量為零的情況下趨於零。這將成為接下來的一個關鍵點。在Gribov的這些研究中，Zwanziger擴展了他的方法。不可避免的結論是，gluon的傳播器應該在瞬間達到零，而在空閒的情況下，幽靈傳播器應該增強。當這個場景被提出時，計算資源不足以決定它是否正確。相反，人們採用了不同的方法，使用了鏑- schwinger方程。這是一組n點函式的耦合方程，它構成了一個層次結構。這意味著n點函式的方程將依賴於(n + 1)-點函式。為了解決它們，我們需要一個適當的截斷。在另一方面，這些方程是非擾動的，可以允許在任何狀態下獲得n點函式的行為。由Reinhard Alkofer、Andreas Hauck和Lorenz von Smekal提出了一種通過截斷來解決這個層次結構的方法。
發展狀況
1972年，在傑勒德·霍oft(Gerard ' t Hooft)之後，楊米爾斯理論得到了物理學界的普遍認可，他們依靠自己的導師馬提尼·維爾特曼(Martinus Veltman)的一個公式來解決他們的重整化問題。(他們的工作獲得了1999年諾貝爾物理學獎。)即使這個理論所描述的標準玻色子是巨大的，如在電弱理論中，只要質量只是一個“獲得的”，由希格斯機制所產生的。
關於數學，應該注意到，目前，在2016年，楊-米爾斯理論是一個非常活躍的研究領域，在西蒙·唐納森的作品中，在四維的流形上具有可微結構的不變性。此外，在陶氏數學研究所的“千年獎問題”列表中，也包括了秧歌理論。這裡的獎項問題在於，尤其在一個猜想的證明中，一個純粹的楊-米爾斯理論(即沒有物質場)的最低興奮度與真空狀態有一個有限的質量差距。另一個與這個猜想有關的開放問題，是在額外的費米子粒子的存在下被限制的性質的證明。
在物理上，對秧歌理論的研究通常不從攝動分析或分析方法開始，而是從系統地套用數值方法到格點理論。
