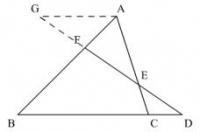梅涅勞斯逆定理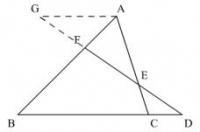

由梅涅勞斯定理得：(AD/DB)*(CE/EA)*(BF/BC)=1因而，由塞瓦逆定理推出AF,BE,CD三線平行或共點顯然矛盾，求解釋.逆定理還是可以用來解決三使用梅涅勞斯定理可以進行直線形中線段長度比例的計算，其逆定理還是可以用來解決三點共線、三線共點等.

簡介

若有三點F、D、E分別在的邊AB、BC、CA或其延長線上，且滿足AF/FB×BD/DC×CE/EA=1，則F、D、E三點共線。利用這個逆定理，可以判斷三點共線。