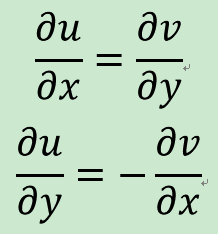柯西-黎曼方程

柯西-黎曼方程，複分析中的柯西-黎曼微分方程是提供了可微函式在開集中為全純函式的充要條件的兩個偏微分方程，以柯西和黎曼得名。

基本信息

• 中文名：柯西-黎曼方程
• 英文名：Cauchy-Riemann Equations

• 屬性：偏微分方程
• 包括：（1a）əu/əx=əv/əy等

簡介

這個方程組最初出現在達朗貝爾的著作中(d'Alembert1752)。後來歐拉將此方程組和解析函式聯繫起來(Euler1777)。然後柯西(Cauchy1814)採用這些方程來構建他的函式理論。黎曼關於此函式理論的論文(Riemann1851)於1851年問世。

方程

柯西-黎曼方程

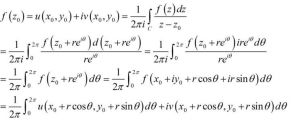在一對實值函式u(x,y)和v(x,y)上的柯西-黎曼方程組包括兩個方程：
(1a)əu/əx=əv/əy和(1b)əu/əy=-əv/əx
柯西-黎曼方程是函式在一點可微的必要條件。
通常，u和v取為一個複函數的實部和虛部：f(x+iy)=u(x,y)+iv(x,y)。假設u和v在開集C上連續可導。則f=u+iv是全純的，若且唯若u和v的偏微分滿足柯西-黎曼方程組(1a)和(1b)。