定律定義
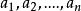 留數定理
留數定理 留數定理
留數定理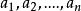 留數定理
留數定理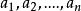 留數定理
留數定理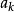 留數定理
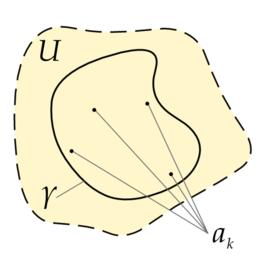
留數定理假設U是複平面上的一個單連通開子集, ,是複平面上有限個點, 是定義在U\{ }的全純函式。如果γ是一條把 包圍起來的可求長曲線,但不經過任何一個 ,並且其起點與終點重合,那么:
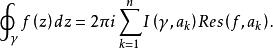 留數定理
留數定理如果γ是若爾當曲線,那么I(γ,ak)=1, 因此:
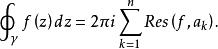 留數定理
留數定理在這裡,Res( f, a)表示 f在點 a的留數,I(γ, a)表示γ關於點 a的卷繞數 。卷繞數是一個整數,它描述了曲線γ繞過點 a的次數。如果γ依逆時針方向繞著 a移動,卷繞數就是一個正數,如果γ根本不繞過 a,卷繞數就是零。
推導過程
以下的積分
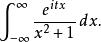 留數定理
留數定理在計算柯西分布的特徵函式時會出現,用初等的微積分是不可能把它計算出來的。我們把這個積分表示成一個路徑積分的極限,積分路徑為沿著實直線從−a到a,然後再依逆時針方向沿著以0為中心的半圓從a到−a。取a為大於1,使得虛數單位i包圍在曲線裡面。路徑積分為:
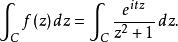 留數定理
留數定理由於eitz是一個整函式(沒有任何奇點),這個函式僅當分母z2 + 1為零時才具有奇點。由於z2 + 1 = (z + i)(z − i),因此這個函式在z = i或z = −i時具有奇點。這兩個點只有一個在路徑所包圍的區域中。
由於f(z)是
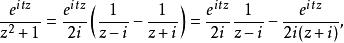 留數定理
留數定理f(z)在z = i的留數是:
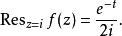 留數定理
留數定理根據留數定理,我們有:
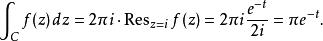 留數定理
留數定理路徑 C可以分為一個“直”的部分和一個曲線弧,使得:
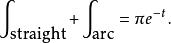 留數定理
留數定理因此
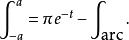 留數定理
留數定理如果 t> 0,那么當半圓的半徑趨於無窮大時,沿半圓路徑的積分趨於零:
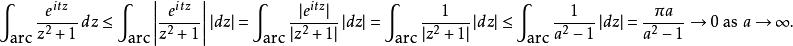 留數定理
留數定理因此,如果 t> 0,那么:
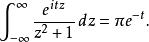 留數定理
留數定理類似地,如果曲線是繞過− i而不是 i,那么可以證明如果 t< 0,則
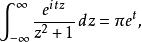 留數定理
留數定理因此我們有:
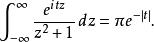 留數定理
留數定理(如果 t= 0,這個積分就可以很快用初等方法算出來,它的值為π。)
相關術語
•路徑積分
•莫雷拉定理
•傅立葉變換
•拉普拉斯變換