測定基礎
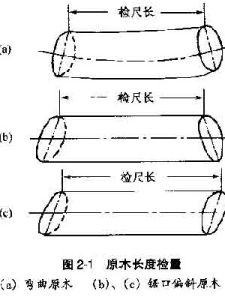 材積
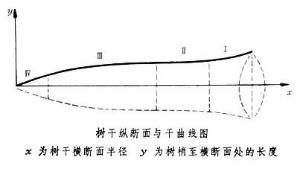
材積為了分析樹幹形狀,可沿樹幹量測許多橫斷面的直徑,以直角坐標的x軸作為樹幹軸。以y軸表示橫斷面的半徑,按適當比例作圖,即可得出表示樹幹縱斷面輪廓的對稱曲線,通稱為乾形曲線(見圖)。這條曲線的線型比較複雜,而且變化不定,自基部向梢端的變化大體呈凹曲線、平行於x軸的直線、拋物線和相交於x軸的直線(如圖中的Ⅰ、Ⅱ、Ⅲ、Ⅳ各段曲線),這4種曲線類型在樹幹上雖無明顯界線,但在不同樹幹上的相對位置是比較穩定的。如果把樹幹看成是乾形曲線以x為軸的鏇轉體,則相應於4部分曲線的體型依次為近似凹曲線體、圓柱體、截頂拋物線體和圓錐體。
德國學者M.孔策1873年提出能分別表達上述幾種線型的乾形曲線式:y2=pxr
式中y為樹幹橫斷面半徑;x為樹梢至該橫斷面處的長度;p為參數;r為形狀指數。形狀指數r一般變化在0~3之間,通常乾基部分為凹曲線體(r≈3),向上依次為近似圓柱體(r≈0),拋物體(r≈1)和圓錐體(r≈2)。利用孔策乾形曲線,根據鏇轉體求積式可以分別求算出樹幹某一段的材積。還曾出現過其他許多表達整株乾形曲線的經驗式,或採用樣條函式分段擬合乾形曲線的方法。
在測樹工作實踐中,常引進削度、形數、形率等乾形數量指標求算樹幹材積和分別指標等級編制材積表,這些指標的含義如下述。
削度(T)樹幹自上而下逐漸減小的程度。分絕對削度和相對削度。絕對削度是樹幹上相距1米兩端直徑之差。相對削度通常以胸徑(d1.3)為100,其他各斷面之直徑(di)與其相比的百分數。削度值的大小直接影響材積和出材率。
 材積
材積形數(f)樹幹材積與比較圓柱體之比。該圓柱體的高等於樹高。按圓柱體所取橫斷面在樹幹上的位置可分胸高形數、正形數。胸高形數(f1.3)以樹幹胸高斷面作為比較圓柱體的橫斷面所計算的形數。正形數(f1/10)以樹幹基部1/10樹高處橫斷面為準計算的形數。最常用的是f1.3,它的大小反映了樹幹粗度變化的快慢。胸高形數、胸高斷面積和樹幹高度三者的乘積就是樹幹材積。
形率(q)樹幹上某一直徑與比較直徑之比。常用的是胸高形率(q2),指樹幹中央直徑(d1/2)與胸徑(d1.3)之比。由於這一因子可通過直徑量測取得,又與f1.3存在緊密相關關係,所以常根據各種回歸式由q2推算f1.3。如f1.3=q2,f1.3=q2+c等。式中c為一常數。
測定方法
 1
1大批量測定樹幹材積,可根據所測定的立木胸徑(樹高1.3米處的樹幹直徑)和樹高或原木的小頭直徑和材長分別查相應的立木或原木材積表即得。板方材按實測長、寬、厚相乘或查板方材積表而得。單株伐倒木、單株立木樹幹材積,薪炭材材積計算法介紹如下。
伐倒木樹幹材積,常用計算方法有:
①中央斷面求積式,也稱胡伯爾公式:V=
量測樹幹長
、在1/2
處量測直徑
,計算出斷面積
,代入公式求算材積
。
②平均斷面求積式,也稱斯馬林公式:
 材積
材積用於截頂樹的量測,分別測定大頭直徑
和小頭直徑
,並求得斷面積
和
。
③截頂拋物體、圓錐體和凹面體求積式,也稱牛頓公式或里克公式:
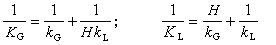 材積
材積利用此式需量測大頭,中央和小頭3處直徑。
④赫斯菲爾德公式:
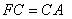 材積
材積量測樹長1/3處直徑和小頭直徑。若取帶梢樹幹,則
=0,公式變為:
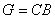 材積
材積⑤按區分段計算材積公式:按一定長度
(一般為1米或2米)把樹幹分成若干段,分別量測每段的中央直徑,並量梢頭底直徑和梢長。
 材積
材積式中
、
……為各區分段材積,
′、
′、
′分別為梢頭材積、梢頭長、梢頭底面積。
單株立術材積,常用的計算公式有:
①胸高形數法:
=
式中
為樹幹材積;
為胸高斷面積;
為樹高;
為胸高形數。形數一般是根據大量伐倒木的實測數據取得,經過數理統計整理,求得實驗回歸式,編制出不同樹種各直徑和樹高的形數表,在計算材積時查用。
②實驗形數法:
=
(
+3)
實驗形數
是根據大量資料的分析而得出的一個經驗係數,它隨樹高的變化要比胸高形數穩定得多,大部分樹種的
集中在0.40~0.44之間。使用時可根據具體情況作常數對待。
③望高法:
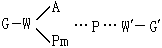 材積
材積式中
為望高(樹幹基部至上部直徑等於1/2胸徑處的高度);
為測點高(即胸高1.3米,若從採伐點算起則為1.0米)。此法不需要測定全樹高,只用儀器(如速測鏡)找到等於1/2胸徑處並測出
便可計算材積。
④丹琴略算法:
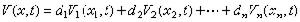 材積
材積,對計算樹高25~30米時的材積較為可靠。
薪炭材材積測定,一般不用單根檢尺的方法測定材積,而把它們截成一定長度後堆放成垛,根據所占空間計算一垛的材積。按垛的長、寬、高所計算的空間體積稱層積材積,扣除材間空隙而求得的木材體積稱實積材積。層積材積可通過換算係數計算出實積材積。換算係數的大小與材積的直徑、彎曲和枝節有關。簡易測定方法有:
①相片網點測定法。將所要測定的木材垛橫斷面拍成相片,復蓋網點板。統計木材斷面上所落點數與總點數的比例,即為實積係數。
②對角線比例測定法。在材垛的正面劃一個與垛高相等的長方形,在長方形兩對角線各牽一皮尺,沿皮尺在各木材頭上用粉筆劃一條線,量測材頭截線的總長度與對角線長度之比即為實積係數。
