簡介
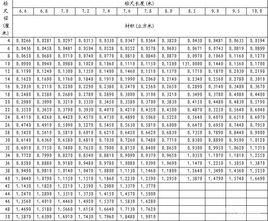
材積表(volume table)是木材計量用表,測樹數表的一種。按計量的對象有原木、立木和原條材積表;
對於鋸材還有計量板方材材積表。板方材材積表是用長、寬、厚的乘積製成,比較簡單。原木、原條和立木材積表是通過研究和建立材積與其他各因子的相關關係,把難以測定的材積指標表示為容易量測的粗度、長度等因子的函式形式,列出相關數表,供計量材積時查用。表中所列數值是大量單根木的平均材積值,對某一個體來說,都存在大小不同、有正有負的誤差。因此,使用材積表應以測量許多個體求其總材積為目的,才能保證必要的精度,而且森林面積越大,計量個體越多,總材積的測算精度越高。
發展歷史
木材成為商品的早期,計量方法是粗放的。早在幾百年前,法國用垛(標準垛約128立方英尺,相當於3.62立方米)、德國用兩匹馬牽引一車裝載量為單位計量燒材材積。18世紀中葉,求算材積的數學公式相繼問世,1786年J.G.克呂尼茨以中央斷面積求積式編成了原木材積表(即圓柱體積表)。由於測定中央直徑不便,其後以小頭直徑為準的原木材積表得到迅速發展。19世紀初德國林學家H.V.科塔提出了“樹幹材積取決於胸徑、樹高和乾形”的理論,並於1804年發表了第一個現代形式的立木材積表。中國於17世紀40年代在長江流域創用了龍泉碼價,來評定杉原條的材積和價格。這是中國最早可考的材積表。
分類
原木積表
一般以原木小頭直徑和材長為檢尺因子編制數表和查定原木材積,表列數值多為實際材積。具體編表方法是實測大量原木,用區分求積法求得實際材積,按小頭直徑和材長分組匯總,分析木材段削度規律,用圖解法或數式法調整出材積經驗式計算材積,列成相關數表。中國於1952年編制了第一個全國一般原木材積表。傳統的原木板英尺(長、寬各1英寸,厚1英寸)材積表1825年已在美國紐約州使用了,即按原木小頭直徑和材長預估能鋸出以板英尺為單位的板方材積的數表。
原條積表
通常根據原條中央直徑和長度編制數表和查定原條材積。
立木積表
按查定材積需測立木因子(胸高、樹高、乾形)的數量不同而分三元、 二元和一元材積表;按計算樹木不同部位材積,可分主幹、 全樹(僅含乾、枝)、枝條、樹根、樹皮等材積表,通常未加說明的是指主幹帶皮材積;按地域範圍分一般和地方材積表;按樹種分某一樹種、樹種組和通用材積表。編表方法可分圖解法、形數法和材積式法。圖解法有繪製削度圖、材積曲線、材積直線及材積列線圖等方法,廣泛採用的是材積回歸方程(數學模型)法。編表基礎數據的代表性、準確性、統一性和選用最優秀的數學模型是保證數表精度的關鍵。
計算方法
一元材積表 只根據立木胸徑一個因子編制和查定立木材積的材積表。具有使用簡便的優點,但由於沒有考慮樹高和乾形的變化,適用地域範圍不大,是一種地方材積表。1878年由法國A.格納德提出,繼由瑞士H.畢奧利發展套用,被稱為“塔里夫”表。“塔里夫”詞源阿拉伯語,意為“數表”。因此稱為“塔里夫”表的形式和內容上有很大的差別。為提高精度還發展了以樹高級、地位級、齡組、林型等控制樹高和平型變化,並分別不同等級(類)編制一元材積表的方法。按樹高、地位分級也有多種形式表示。一元材積表在一定區域內採用一個共同的平均材積曲線,而分級(類)編制的一元材積表是給出數條材積曲線,具有二元表的特性。但計量材積的精確度欠佳,經試驗和誤差檢驗,選用距原條底徑 2.5米的直徑為檢尺徑與材長兩因子重新編制了杉原條材積表,1984年作為國家標準頒布使用。
二元材積表 根據立木胸徑和樹高兩個因子編制和查定立木材積的材積表。由於樹木乾形與胸徑、樹高密切相關,不把乾形因子直接作為獨立變數編表,理論誤差不大,因此二元材積表發展較快,並成為多數國家的基本材積表。
三元材積表 根據立木胸徑、樹高和乾形某一指標3 個因子編制和查定立木材積的材積表。乾形指標多採用樹木中央直徑與胸徑之比(形率)。此外還有用胸高以上樹幹高的中央直徑與胸徑之比,枝下高、胸高直徑與上部某一直徑之差,第一段標準原木小頭去皮直徑與胸高帶皮直徑的百分比等來表示。著名的德國格隆德乃爾 -施伐撥帕赫材積表是分別樹種、分別齡組,按胸徑和樹高編制的,劃分齡組具有間接劃分乾形級的作用,因而也有三元表的性質。該表由成材材積表(小頭直徑 7厘米以上的材積)、樹木材積表、枝條材積表、樹皮材積表、削度表、林分形數表、材種表和樹高表組成,被譽為最完備的材積表。
上述各種數表中國均有編制和研究。
數學模型
經常採用的數學模型列舉如下:
材積式:一元材積式:
V=b0D
V=b0+b1D2
二元材積式:
V=b0DH
V=b0+b1D2+b2H+b3D2H
V=b0+b1D2+b2D2H+b3H2
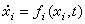 材積表
材積表+b4H2三元材積式:
V=b0DHF
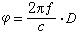 材積表
材積表V=b0+b1FD2H形數式:
以上各式中, D為胸徑, H為樹高; F為乾形指標(代數、形率、直徑差、直徑比等); f為胸高形數, bi為參數; e為自然對數的底; B為樹皮厚度; K為枝下高率; m為常數; H′為胸高。