有限時間區間穩定性
正文
系統受到初始擾動後的運動相對於一個確定的時間區間內的穩定性。這類穩定性的研究主要針對那些不能用特徵值（見狀態空間法）判別穩定性的系統，特別是參數隨時間變化的線性時變系統。有限時間區間穩定性問題是1953年蘇聯學者Г.В.卡曼科夫提出的。有限時間區間穩定性問題的研究結果可用於判斷：當擾動引起的初始受擾運動限制在某個範圍內時，系統的受擾運動在一個確定的時間區間內是否會越出規定的誤差範圍。對於線性時變系統，有限時間區間穩定性的定義可表述為：給定系統的狀態方程dx/dt=A(t)x，其中x為n維狀態向量，A(t)是n×n時變矩陣。如果對給定的正實常數ε和C，當系統狀態的初始擾動 x(t0)滿足||x(t0)||2≤ε的限制時，系統的運動x(t)總是滿足下列條件：
||x(t)||2≤C t0≤t≤T
那么就稱系統對給定的ε和C在有限時間區間 【t0,T】上是穩定的。其中||x(t)||2＝x娝(t)+…x娾(t)，xi(t)是狀態向量x(t)的第i個分量。在工程套用中，常數C和ε通常根據具體問題的實際情況來規定,T是為估計系統受擾運動所需要的時間。判斷有限時間區間穩定性的一個主要結果為：對給定係數矩陣A(t)和常數ε及C，確定一個 時間常數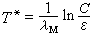
,其中λM是對稱矩陣A(t)+AT(t)在時間區間【t0,T】上的最大特徵值,AT(t)是A(t)的轉置矩陣。當T≤T *時,系統相對於ε和C在【t0,T】上是有限時間穩定的；而當T ＞T *時,不能確定系統是否相對於ε和C 在【t0,T】上為有限時間穩定或不穩定。