釋義
在數學中， 有序偶是兩個對象的蒐集，使得可以區分出其中一個是“第一個元素”而另一個是“第二個元素”（第一個元素和第二個元素也叫做 左投影和 右投影）。帶有第一個元素 a和第二個元素 b的 有序偶通常寫為( a, b)。
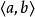有序偶符號( a, b)也表示在實數軸上的開區間；在有歧義的場合可使用符號。
一般性
設( a, b)和( a, b)是兩個 有序偶。則 有序偶的特徵或定義性質為：
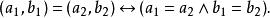有序偶有序偶可以有其他有序對作為投影。所以 有序偶使得能夠遞歸定義有序 n-元組（ n項的列表）。例如，有序三元組 ( a,b,c)可以定義為( a, ( b,c))，一個對嵌入了另一個對。這種方法也反映在計算機程式語言中，就是從嵌套的有序對構造元素的列表。例如，列表 (1 2 3 4 5)變成了(1, (2, (3, (4, (5, {} )))))。Lisp程式語言使用這種列表作為基本數據結構。
有序偶的概念對於定義笛卡爾積和關係是至關重要的。
集合論中定義
諾伯特·維納在1914年提議了 有序偶的第一個集合論定義：
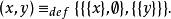有序偶他注意到這個定義將允許《數學原理》中所有類型只透過集合便能表達。
標準Kuratowski定義
在公理化集合論中， 有序偶( a, b)通常定義為庫拉托夫斯基對：
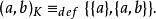有序偶陳述“ x是有序對 p的第一個元素”可以公式化為
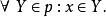有序偶而陳述“ x是 p的第二個元素”為
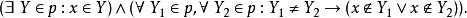有序偶注意這個定義對於 有序偶 p= ( x, x) = { { x}, { x, x} } = { { x}, { x} } = { { x} }仍是有效的；在這種情況下陳述(∀ Y∈ p, ∀ Y∈ p: Y≠ Y→ ( x∉ Y∨ x∉ Y))顯然是真的，因為不會有 Y≠ Y的情況。
變體定義
上述 有序偶的定義是“充足”的，在它滿足 有序偶必須有的特徵性質（也就是：如果( a, b)=( x, y)則 a= x且 b= y）的意義上，但也是任意性的，因為有很多其他定義也是不更加複雜並且也是充足的。例如下列可能的定義
(a,b):= { {b}, {a,b} }
(a,b):= {a, {a,b} }
(a,b):= { {0,a}, {1,b} }
1.(a,b):= { {b}, {a,b} }
2.(a,b):= {a, {a,b} }
3.(a,b):= { {0,a}, {1,b} }
“逆”（reverse）對基本不使用，因為它比通用的Kuratowski對沒有明顯的優點（或缺點）。“短”（short）對有一個缺點，它的特徵性質的證明會比Kuratowski對的證明更加複雜（要使用正規公理）；此外，因為在集合論中數2有時定義為集合{ 0, 1 } = { {}, {0} }，這將意味著2是對 (0,0)。
性質證明
Kuratowski對： 證明：( a,b)= ( c,d)若且唯若 a= c且 b= d。
僅當：
如果 a= b，則 ( a,b)= {{ a}, { a,a}} = { { a} }，且 ( c,d)= {{ c},{ c,d}} = { { a} }。所以{ c} = { a} = { c,d}，或 c=d=a=b。
如果 a≠ b，則{{ a}, { a,b}} = {{ c},{ c,d}}。
如果{ c,d} = { a}，則 c=d=a或{{ c},{ c,d}} = {{ a}, { a,a}} = {{ a}, { a}} = { { a} }。但這樣{{ a}, { a, b}}就會等於{{ a}}，繼而 b = a，跟先前的假設矛盾。
如果{ c} = { a,b}，則 a=b=c，這矛盾於 a≠ b。所以{ c} = { a}，即 c=a，且{ c,d} = { a,b}。
並且如果 d=a，則{ c,d} = { a,a} = { a}≠{ a,b}。所以 d=b。
所以同樣有 a=c且 b=d。
當：
反過來，如果 a=c並且 b=d，則顯然{{ a},{ a,b}} = {{ c},{ c,d}}。所以 ( a,b)= ( c,d)。
逆對： ( a,b)= {{ b},{ a,b}} = {{ b},{ b,a}} = ( b,a)。
如果 ( a,b)= ( c,d)，則 ( b,a)= ( d,c)。所以 b=d且 a=c。
反過來，如果 a=c和 b=d，則顯然{{ b},{ a,b}} = {{ d},{ c,d}}。所以 ( a,b)= ( c,d)。
Quine-Rosser定義
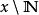有序偶Rosser（1953年）擴展了蒯因的 有序偶定義。Quine-Rosser的定義要求自然數的先決定義。設N是自然數的集合，是N在x內的相對差集，並定義：
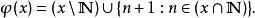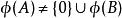有序偶
有序偶φ( x)包含在 x中所有自然數的後繼，和 x中的所有非數成員。特別是，φ( x)不包含數0，所以對於任何集合 A和 B，。
以下是有序對 ( A, B)的定義：
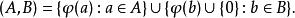有序偶
有序偶提取這個對中那些不包含0的所有元素，然後再還原的作用，就得出了 A。類似的， B可以通過提取這個對的包含0的所有元素來復原。
有序偶的這個定義有個顯著的優點。在類型論和從類型論派生出的集合論如新基礎中，這個對與它的投影有相同的類型（所以術語叫做“類型齊平”有序對）。因此一個函式（定義為 有序偶的集合），有隻比序對的投影的類型高1的類型。
Morse定義
Morse（1965年）提出的Morse-Kelley集合論可以自由的使用真類。Morse定義有序對的方法，使得它的投影可以是真類或者集合。（Kuratowski定義不允許這樣）。它首先像Kuratowski的方式那樣，定義投影為集合的 有序偶。接著，他 重定義對 ( x, y)為
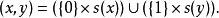有序偶這裡的笛卡爾積是指由Kuratowski對組成的集合併且
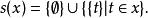有序偶這便允許了定義以真類為投影的 有序偶。
參見
•笛卡兒積
•二元關係
