概述
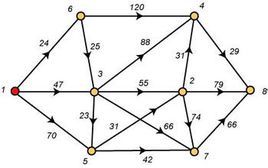
 最短路徑
最短路徑確定起點的最短路徑問題 - 即已知起始結點,求最短路徑的問題。
確定終點的最短路徑問題 - 與確定起點的問題相反,該問題是已知終結結點,求最短路徑的問題。在無向圖中該問題與確定起點的問題完全等同,在有向圖中該問題等同於把所有路徑方向反轉的確定起點的問題。
確定起點終點的最短路徑問題 - 即已知起點和終點,求兩結點之間的最短路徑。
全局最短路徑問題 - 求圖中所有的最短路徑。
解決方法
基本綜述
用於解決最短路徑問題的算法被稱做“最短路徑算法”,有時被簡稱作“路徑算法”。最常用的路徑算法有:
Dijkstra算法
A*算法
SPFA算法
Bellman-Ford算法
Floyd-Warshall算法
Johnson算法
所謂單源最短路徑問題是指:已知圖G=(V,E),我們希望找出從某給定的源結點S∈V到V中的每個結點的最短路徑。
首先,我們可以發現有這樣一個事實:如果P是G中從vs到vj的最短路,vi是P中的一個點,那么,從vs沿P到vi的路是從vs到vi的最短路。
Dijkstra算法
Dijkstra(迪傑斯特拉)算法是典型的最短路徑路由算法,用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴展,直到擴展到終點為止。Dijkstra算法能得出最短路徑的最優解,但由於它遍歷計算的節點很多,所以效率低。
Dijkstra算法是很有代表性的最短路算法,在很多專業課程中都作為基本內容有詳細的介紹,如數據結構,圖論,運籌學等等。
Dijkstra一般的表述通常有兩種方式,一種用永久和臨時標號方式,一種是用OPEN,CLOSE表方式,Drew為了和下面要介紹的A*算法和D*算法表述一致,這裡均採用OPEN,CLOSE表的方式。
其採用的是貪心法的算法策略
大概過程:
OPEN表保存所有已生成而未考察的節點,CLOSED表中記錄已訪問過的節點。
1.訪問路網中距離起始點最近且沒有被檢查過的點,把這個點放入OPEN組中等待檢查。
2.從OPEN表中找出距起始點最近的點,找出這個點的所有子節點,把這個點放到CLOSE表中。
3.遍歷考察這個點的子節點。求出這些子節點距起始點的距離值,放子節點到OPEN表中。
4.重複第2和第3步,直到OPEN表為空,或找到目標點。
用C語言描述Dijkstra算法
voidShortest_DIJ(MGraphG,intv0,PathMatrix&p,ShortPathTable&d)
//用Dijkstra算法求有向網G的v0頂點到其餘頂點v的最短路徑p[v]及其帶權長度d[v]
//若p[v][w]為TRUE,則w是從v0到v當前求得最短路徑上的頂點
//final[v]為TRUE若且唯若v屬於s,記已經求得從v0到v的最短路徑
for(v=0;v權值" for(w="0;wclass="boldColor margin_border yellow_red">最近的點
for(w=0;w