元啟發式算法
計算機科學的兩大基礎目標,就是發現可證明其執行效率良好且可得最佳解或次佳解的算法。而啟發式算法則試圖一次提供一或全部目標。 例如它常能發現很不錯的解,但也沒辦法證明它不會得到較壞的解;它通常可在合理時間解出答案,但也沒辦法知道它是否每次都可以這樣的速度求解。有時候人們會發現在某些特殊情況下,啟發式算法會得到很壞的答案或效率極差,然而造成那些特殊情況的數據結構,也許永遠不會在現實世界出現。因此現實世界中啟發式算法常用來解決問題。啟發式算法處理許多實際問題時通常可以在合理時間內得到不錯的答案。
有一類的通用啟發式策略稱為元啟發式算法(metaheuristic algorithm),通常使用亂數搜尋技巧。他們可以套用在非常廣泛的問題上,但不能保證效率。
算法原理
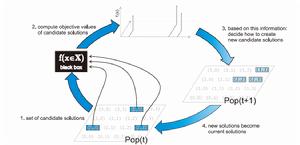
1. 從一個或多個候選解開始作為初始值(pop(t))。2. 根據初始值計算目標函式值
3. 基於已獲得的信息,通過個體變異、組合等方法不斷更新候選解域。
4. 新的候選解域進入下一輪疊代(pop(t+1))
如下圖:
編程分析
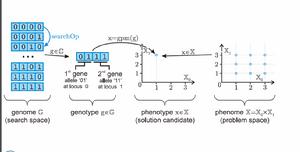
從程式的角度分析,元啟發式算法包括以下幾個部分:1. 內部數據結構G,用於描述候選解域X中的候選解。
2. 從數據結構G,創建候選解實例的法則。
3. 如果G ≠ X,需要定義一個函式g2x(),該函式用於將結果從G域映射到X域,g2x()函式往往對結果直接產生較大的影響。
4. 用於改變候選解的算法,如變異,交叉等。
5. 整體循環流程控制函式。
過程圖解如下
下圖為算法疊代流程: