Dijkstra算法
問題描述
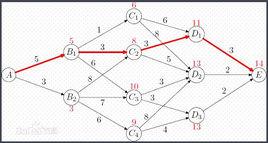
給定一個帶權有向圖 G=(V,E) ,其中每條邊的權是一個 非負實數。另外,還給定 V 中的一個頂點,稱為源。現在我們要計算從源到所有其他各頂點的最短路徑長度。這裡的長度是指路上各邊權之和。這個問題通常稱為單源最短路徑問題。
Dijkstra算法的解決方案
Dijkstra提出按各頂點與源點v間的路徑長度的遞增次序,生成到各頂點的最短路徑的算法。既先求出長度最短的一條最短路徑,再參照它求出長度次短的一條最短路徑,依次類推,直到從源點v 到其它各頂點的最短路徑全部求出為止。
Dijkstra算法的解題思想
將圖G中所有的頂點V分成兩個頂點集合S和T。以v為源點已經確定了最短路徑的終點併入S集合中,S初始時只含頂點v,T則是尚未確定到源點v最短路徑的頂點集合。然後每次從T集合中選擇S集合點中到T路徑最短的那個點,並加入到集合S中,並把這個點從集合T刪除。直到T集合為空為止。
具體步驟
1、選一頂點v為源點,並視從源點v出發的所有邊為到各頂點的最短路徑(確定數據結構:因為求的是最短路徑,所以①就要用一個記錄從源點v到其它各頂點的路徑長度數組dist[],開始時,dist是源點v到頂點i的直接邊長度,即dist中記錄的是鄰接陣的第v行。②設一個用來記錄從源點到其它頂點的路徑數組path[],path中存放路徑上第i個頂點的前驅頂點)。
2、在上述的最短路徑dist[]中選一條最短的,並將其終點(即<v,k>)k加入到集合s中。
3、調整T中各頂點到源點v的最短路徑。 因為當頂點k加入到集合s中後,源點v到T中剩餘的其它頂點j就又增加了經過頂點k到達j的路徑,這條路徑可能要比源點v到j原來的最短的還要短。調整方法是比較dist[k]+g[k,j]與dist[j],取其中的較小者。
4、再選出一個到源點v路徑長度最小的頂點k,從T中刪去後加入S中,再回去到第三步,如此重複,直到集合S中的包含圖G的所有頂點。
解決方案
pascal:
c++:
c:
Bellman-Ford算法
描述
由於Dijikstra算法對於帶負邊權的圖就無能為力了,但是Bellman-Ford算法就可以解決這個問題。
Bellman-Ford的解題思想
算法基於動態規劃,反覆用已有的邊來更新最短距離,Bellman-Ford算法的核心思想是鬆弛。如果dist[u]和dist[v]滿足dist[v]>dist[u]+map[u][v],dist[v]就應該被更新為dist[u]+map[u][v]。反覆的利用上式對dist數組進行鬆弛,如果沒有負權迴路的話,應當會在n-1次鬆弛後結束。
Bellman-Ford算法的偽代碼
s為源,map[][]記錄圖的信息,map[u][v]為點u到v的邊的長度,結果保存在dist[];
初始化,所有點 i 賦初值dist[i] =+無窮大,出發點為s,dist[s]=0;
對於每條邊(u,v),如果dist[u]!=+無窮大且dist[v]>dist[u]+map[u][v],則dist[v]=dist[u]+map[u][v].
循環步驟2n-1次或直到某次中不在更新,進入步驟4.
對於每條邊(u,v),如果dist[u]!=+無窮大且dist[v]>dist[u]+map[u][v],則存在負權迴路。
1.初始化,所有點 i 賦初值dist[i] =+無窮大,出發點為s,dist[s]=0;
2.對於每條邊(u,v),如果dist[u]!=+無窮大且dist[v]>dist[u]+map[u][v],則dist[v]=dist[u]+map[u][v].
3.循環步驟2n-1次或直到某次中不在更新,進入步驟4.
4.對於每條邊(u,v),如果dist[u]!=+無窮大且dist[v]>dist[u]+map[u][v],則存在負權迴路。
c:
SPFA算法
描述
SPFA(Shortest Path Faster Algorithm)算法是求單源最短路徑的一種算法,在Bellman-ford算法的基礎上加上一個佇列最佳化,減少了冗餘的鬆弛操作,是一種高效的最短路算法。在 NOI2018Day1T1歸程 中正式被卡,其時間複雜度為O(nm),遠劣於Dijkstra的O((n+m)log m)。
SPFA算法的解題思想
我們約定加權有向圖G不存在負權迴路,即最短路徑一定存在。如果某個點進入佇列的次數超過N次則存在負環(SPFA無法處理帶負環的圖)。當然,我們可以在執行該算法前做一次拓撲排序,以判斷是否存在負權迴路,但這不是我們討論的重點。我們用數組d記錄每個結點的最短路徑估計值,而且用鄰接表來存儲圖G。我們採取的方法是動態逼近法:設立一個先進先出的佇列用來保存待最佳化的結點,最佳化時每次取出隊首結點u,並且用u點當前的最短路徑估計值對離開u點所指向的結點v進行鬆弛操作,如果v點的最短路徑估計值有所調整,且v點不在當前的佇列中,就將v點放入隊尾。這樣不斷從佇列中取出結點來進行鬆弛操作,直至佇列空為止。定理: 只要最短路徑存在,上述SPFA算法必定能求出最小值。
SPFA算法的偽代碼
SPFA實際上是Bellman-Ford基礎上的佇列最佳化
SPFA(G,w,s)
1. INITIALIZE-SINGLE-SOURCE(G,s)
2. INITIALIZE-QUEUE(Q)
3. ENQUEUE(Q,s)
4. While Not EMPTY(Q)
5. Do u<-DLQUEUE(Q)
6. For 每條邊(u,v) in E[G]
7. Do tmp<-d[v]
8. Relax(u,v,w)
9. If (d[v] < tmp) and (v不在Q中)
10. ENQUEUE(Q,v)
c++:
boolSPFA(intsource)
{
deque<int>dq;
inti,j,x,to;
for(i=1;i<=nodesum;i++)
{
in_sum[i]=0;
in_queue[i]=false;
dist[i]=INF;
path[i]=-1;
}
dq.push_back(source);
in_sum[source]++;
dist[source]=0;
in_queue[source]=true;
//初始化完成
while(!dq.empty())
{
x=dq.front();
dq.pop_front();
in_queue[x]=false;
for(i=0;i<adjmap[x].size();i++)
{
to=adjmap[x][i].to;
if((dist[x]<INF)&&(dist[to]>dist[x]+adjmap[x][i].weight))
{
dist[to]=dist[x]+adjmap[x][i].weight;
path[to]=x;
if(!in_queue[to])
{
in_queue[to]=true;
in_sum[to]++;
if(in_sum[to]==nodesum)
return false;
if(!dq.empty())
{
if(dist[to]>dist[dq.front()])
dq.push_back(to);
else
dq.push_front(to);
}
else
dq.push_back(to);
}
}
}
}
returntrue;
}