國中
以數軸為載體,不再贅述,見下面問題
已知,如圖,A.B分別為數軸上的兩點,A點對應的數為-20,B點對應的數為100.
(1)請寫出AB中點M對應的數.
——A -30————————————B 100——(此為直線圖)
(2)現有一隻電子螞蟻P從B點出發,以5單位/秒的速度向左運動,同時另一支電子螞蟻Q橋好從A點出發,以3單位/秒的速度向右運動,設兩隻電子螞蟻在數軸上的C點相遇,你知道C點對應的數是多少嗎?
(3)若當電子螞蟻P從B點出發時,以5單位/秒的速度向左運動,同時另一支電子螞蟻Q恰好從A點出發,以3單位/秒的速度也向左運動,設電子螞蟻P在數軸上的D點追上電子螞蟻Q,你知道D點對應的數是多少嗎?
第一問
(30+100)÷2=65
第二問
設象→為正方向,向←為負方向。設經過的時間為t
電子螞蟻Q的坐標公式應該為
X=-30+3t
電子螞蟻P的坐標公式應該為
y=100-5t
兩隻螞蟻相遇時,即指兩隻螞蟻的位置相同,即坐標相同,於是有等式:
x=y
帶入
-30+3t=100-5t
t=65/4(s)
所以y=100-5*65/4=25
所以c點對應數為245/4.
同理第三問
x=-30-3t
y=100-5t
x=y
所以
-30-3t=100-5t
t=65S
所以y=100-5*65=-225
所以D點對應數為-225
高中
平面定軌路徑最短
 路徑最短組合
路徑最短組合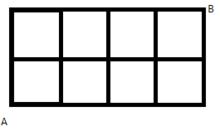 路徑最短組合
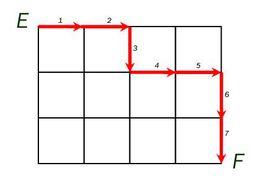
路徑最短組合根源:坐標系中有一電子螞蟻在原點,無返回,只能沿x、y正方向爬,爬到(m,n)的所有路徑總數為 如圖,實線為街道,一人需從A到B,則路程最短的走法有幾種?
解析:將問題抽象不難得到15種
幾何體表面兩點間
最短路徑問題
最短路徑問題是圖論研究中的一個經典算法問題, 旨在尋找圖(由結點和路徑組成的)中兩結點之間的最短路徑。 算法具體的形式包括:
確定起點的最短路徑問題 - 即已知起始結點,求最短路徑的問題。
確定終點的最短路徑問題 - 與確定起點的問題相反,該問題是已知終結結點,求最短路徑的問題。在無向圖中該問題與確定起點的問題完全等同,在有向圖中該問題等同於把所有路徑方向反轉的確定起點的問題。
確定起點終點的最短路徑問題 - 即已知起點和終點,求兩結點之間的最短路徑。
全局最短路徑問題 - 求圖中所有的最短路徑。
解決方法:只需將幾何體展開分別計算距離比較即可
註:如若是球,則取過球心的最大圓,兩點間的短弧長即為所求