概述
最小作用量原理作為研究光線的反射和折射的結果，費爾馬曾得出這樣的結論：“自然界總是通過最短的途徑發生作用的。”此後，莫培督在其1744年的一片著名論文中宣布了一個原理，他稱之為“最小作用量原理。”他用這樣幾句話說明了這個原理：“自然界總是通過最簡單的方法產生起作用的。如果一個物體必須沒有任何阻礙地從這一點到另一點——自然界就利用最短的途徑和最快的速度來引導它。”（原先也一直不能並存的自然界各種規律現在就一致起來了。《科學院的報告》，1744年4月15日，第421頁）簡單地說這意味著任何不受費爾馬
影響的動力學系統在發生變化時，其變化方式總是使有關的作用量為最小。在對物理實在（現象）的觀察中，科學家們相信，對於不同的觀察者物理實在可以不同，但其物理實在的結構（規律）必定是相同的。物理學中描述物理實在結構的方法之一就是作用量方法。這種方法從功能角度去考察和比較客體一切可能的運動（經歷），認為客體的實際運動（經歷）可以由作用量求極值得出，是其中作用量最小的那個。這個原理稱為最小作用量原理。動力學中的一個變分原理。由保守系統的動力方程可以導出這個原理，也可自這原理導出動力方程。這原理可表述為：對於定常保守系統,作用量TDT的積分的全變分為零。即(1)式中T為動能;t為時間；Δ為全變分記號。Δ與變分記號δ不同之處是：δt＝0，而Δt厵0。將Δ與δ施於同一變數時，有關係式：Δqi=δqi+妜iΔt。因此Δ和δ兩符號有關係式：。最小作用量原理還可詳述為：對於定常保守系統，在廣義坐標qi和時間t的聯合空間(q1,q2,…,qN;t)里,對於機械能E保持不變（即δE＝0)的各條路徑中,如果路徑的端點（包括始點和終點）的全變分為零,則積分對於真實運動的路徑和鄰近的旁路比較，真實路徑的積分是駐值。在一般實際情況中，式(1)確定的積分為極小值，最小作用量原理即由此得名。對於一個質點，，因此式（1）成為上式是1744年由馬保梯最先提出的一個最小作用量原理。他研究這個問題的目的是想配合光學中的費馬原則,說明光是一種高速運動著的微粒。L.-V.德布羅意和E.薛丁格等所創立的波動力學（現在都稱它為量子力學）也受到力學中的最小作用量原理和光學中的費馬原理的許多類似之處的啟發。後來L.歐拉證明這原理對於一個質點在有心力場中的運動也是成立的。J.-L.拉格朗日把這原理推廣到N個自由度的保守系統並給予嚴格證明，所以這原理稱為馬保梯－拉格朗日最小作用量原理。
原理簡介
動力學中的一個變分原理。由保守系統的動力方程可以導出這個原理，也可自這原理導出動力方程。這原理可表述為：對於定常保守系統,作用量Tdt的積分的全變分為零。即
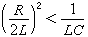(1)
Δqi=δqi+妜iΔt。
因此Δ和δ兩符號有關係式：。
最小作用量原理還可詳述為：對於定常保守系統，在廣義坐標qi和時間t的聯合空間(q1,q2,…,qN;t)里,對於機械能E保持不變（即δE＝0)的各條路徑中,如果路徑的端點（包括始點和終點）的全變分為零,則積分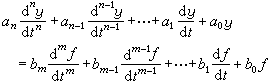
對於真實運動的路徑和鄰近的旁路比較，真實路徑的積分是駐值。在一般實際情況中，式(1)確定的積分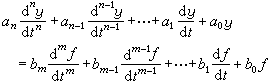為極小值，最小作用量原理即由此得名。 對於一個質點，
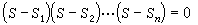，因此式（1）成為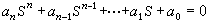 
上式是1744年由 P.-L.M.de馬保梯最先提出的一個最小作用量原理。他研究這個問題的目的是想配合光學中的費馬原則,說明光是一種高速運動著的微粒。L.-V.德布羅意和E.薛丁格等所創立的波動力學（現在都稱它為量子力學）也受到力學中的最小作用量原理和光學中的費馬原理的許多類似之處的啟發。後來L.歐拉證明這原理對於一個質點在有心力場中的運動也是成立的。 J.-L.拉格朗日把這原理推廣到N個自由度的保守系統並給予嚴格證明，所以這原理稱為馬保梯－拉格朗日最小作用量原理。
最小作用量原理與哈密頓原理的相同點是：①兩者都是作用量的積分的變分原理,對時間不長的運動,兩者都是極小值；②兩者都是在多維空間(q1,q2,…,qN;t)中真實路線積分與旁路線積分的比較；③這兩個原理在所設條件下與保守系統的動力方程等效，三者可互相推導。最小作用量原理與哈密頓原理的不同點是:①哈密頓原理以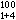
為作用量,L為動勢,最小作用量原理以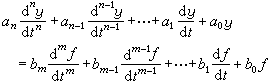為作用量；②哈密頓原理的始點和終點在多維空間(q1，q2,…,qN；t)中為兩定點,變分為等時的,即δt=0,最小作用量原理的始點q0和終點q1的全變分為零。即Δq0＝Δq1=0，且機械能E在各條路線上相同，即δE＝0。兩種作用量有關係式： 式中H為哈密頓函式。
數學描述
費 德布羅意principleofleastaction機械能守恆系統[1]在位形空間真實軌道上運動時所遵循的一個基本原理。二倍動能T對時間dt的積分稱為拉格朗日作用量2Tdt。在N維位形空間(q1，q2，…，qN)中，表示點沿著具有相同機械能的端點的真實路徑上的作用量和沿鄰近的可能路徑上的作用量比較，沿真實路徑的作用量取駐值(包括極值)。考慮在N維q空間自始點A(q10，q20，…，qN0)出發的兩條運動的真實路徑，這兩條路徑是相鄰的，只是出發的方向略有不同。這兩條路徑除A外可能還有其他交點，若B是靠近A的第一個交點(見圖)。當兩條路徑的出發方向趨於一致時，B的極限點稱為動焦點。當代表點的路徑長超過時，作用量積分既非極小也非極大。長度不超過始點和第一個動焦點之間的路徑長時，真實路徑的作用量是極小值。拉格朗日作用量S＝2Tdt同哈密頓作用量w＝Ldt（見哈密頓原理）的關係式為 w＝S-H(t2-t1)，H為哈密頓函式。在空間運動的質點的作用量為 S＝2Tdt＝мv2dt＝мvds。於是質點運動的最小作用量原理可用變分表示為 δvds＝0。
上式是莫培督在1744年提出來的最小作用量原理的表示式。他是受到17世紀時期所建立的
馬原理啟發，用微粒說來解釋光在空間的行進規律。L.歐拉認為這個原理很有價值，在1744年用力學方法證明它在輳力場中成立。對質點系的最小作用量原理的證明是J.L.拉格朗日在1760年得出的。在物理學上，微粒和波動的對偶關係是L.V.德布羅意在1923年提出物質波後，再經過C.J.戴維孫和L.H.革末於1927～1928年的實驗所證實，才得到公認的。德布羅意就是在費馬原理和最小作用量原理的啟發下發展了物質波理論。
近代發展
莫佩爾蒂莫佩爾蒂於1744年發表了最小作用量原理。這原理闡明，對於所有的自然現象，作用量趨向於最小值。他定義作用量為物體的質量，移動距離，與移動速度的乘積。1741年，莫佩爾蒂在巴黎科學院發表了一篇論文，"Loidureposdescorps"，（靜止物體定律）。他表明，在一個系統里，所有呈靜止狀態的物體，假若有任何變化，產生的運動，趨向於作用量的最小改變。在另一篇於1744年，在巴黎科學院發表的論文中，他提出了"Accorddeplusieursloisnaturellesquiavaientparujusqu'iciincompatibles"（幾種以前互不相容的自然定律的合一論)：光折射的路徑，從一種介質到另一種介質，是作用量的最小值。1746年，莫佩爾蒂更進一步地在伯林科學院發表了論文，"Loixdumouvementetdurepos"（運動與靜止定律）。他表明，質點的運動也趨向於最小作用量。為了便於分析，物體的全部質量可以被視為集中於一點，稱這一點為質點。在十八世紀前期，關於質點經碰撞後的可能發生狀況，有很大的爭論。笛卡兒派與牛頓派物理學家認為，在碰撞下，幾個質點的總動量與相對速度是恆定的。萊布尼茨派則認為活力(visviva)也莫佩爾蒂
是恆定的。由於兩個原因，這論點是笛卡兒派與牛頓派無法接受的:1.活力恆定不能套用於硬物體（不能壓縮的物體）。2.活力的數學定義是質量與速度平方的乘積。為什麼速度在活力這數量里出現兩次？萊布尼茨派辯明，理由很簡單，任何物質對於運動都有一種自然的趨向。在靜止狀態，物體裡含有一個內在的速度。當物體開始移動時，對應於實際的運動，又產生了第二個速度項目。笛卡兒派與牛頓派則認為這辯理簡直是胡言。對於中古學者，運動的內在趨向這句話，具有一種奧秘的性質；這中古學者的偏愛，必須毫無反顧地抗拒。今天，硬物體的概念已被完全地否定了。至於質量與速度平方的乘積，這數量則是動能的兩倍。現代力學給予了活力一個很重要的角色。對於莫佩爾蒂而言，硬物體的概念是很重要的。他提出的最小作用量原理有一個很特別的優點：這原理可以套用於硬物體與彈性物體。又可以套用於靜止狀態的物體與光，似乎，這原理可以廣泛的套用於宇宙的每一個角落。莫佩爾蒂又從宇宙論的觀點來論述：最小作用量好像一個經濟原理；在經濟學裡，大概就是精省資源的意思。這論述的瑕疵是，並沒有任何理由，能夠解釋，為什麼作用量趨向最小值，而不是最大值。事實上，萊布尼茨證明過，在大自然現象中，這物理量有可能趨向最小值，也有同樣的可能趨向最大值。假若，我們解釋最小作用量為大自然的精省資源，那么，我們又怎么解釋最大作用量呢？在量子力學的發展中，作用量的不連續性不以其最初的假定方式保持下來。這種不連續性使解釋量子力學的數量關係成為可能，但卻沒有去找這種解釋。這樣，不連續性就以終極概念的身份出現了。作用量不連續在日後推廣為相對論的量子論中可以得到因果性的解釋。看來這種推廣的嘗試對作用量概念本身帶來某些新的認識，就像時空格線數的概念那樣，用普朗克常數去除作用量的表象沒有被排除，嬗變過程就在此格線中發生，在巨觀的近似中格線可以作為自身同一的基本粒子的世界線而加以研究。此時世界線的機率就同愛丁頓所說的那種數量關係的作用量聯繫在一起，於是最小作用量原理就成為最大機率原理。1819年，高斯在題為《論新的力學普遍原理》一書中，提出了作為更為普遍原理的結論，無摩擦的約束系統在任意力作用下將這樣運動：來自約束的對系統的拘束和施加於約束上的壓力均取極小值。高斯用以下方式闡述了他的最小拘束原理。“倘若質點是自由的，那么對以任何方式聯繫起來的，受任意影響的質點系來說，它在每一時刻的運動都要完全或只是有可能完全依照這些質點本來就有的方式進行活動，也就是說運動要以儘可能小的拘束進行。如果在無限小的瞬間，對每一質點的質量和該質點現在的位置的偏離量的平方之積取和，這個和則可作為對拘束的量度高斯觀念的發展是1892——1893年赫茲提出的最直路徑原理。這個原理同時延續了雅考畢的思路，即對全部變分原理和動力學加以幾何化。這一問題在眾所周知，赫茲不用力的概念而要建立起力學的嘗試中得到闡明。這個嘗試是在《力學原理》這本書上講的（1892）。[羅素的某些看法。根據質量和能量的相對論的數量關係，羅素推出把質量和時間之積當成作用量的可能性。但是，引力質量還有與其相等的慣性質量可以由距離代表，這時作用量就是長度和時間的乘積了。用這種觀點來看待普朗克常量，羅素說：要是把作用量取作物理學的基本概念，我們或許能建立起來全是原子論的，極適於檢驗的物理學。羅素接著指出：相對論中時間空間間隔的不變性和作用量的意義（即在微觀世界中的作用量）之間的聯繫是意味深長的。與上述類似的一些構想並不能引起物理知識的實際的進展，不過卻很值得提出來，因為此後推廣量子力學時要用作用量來表征近代物理的特徵和風格。
折射理論
於1744年，在巴黎科學院發表的一篇論文《幾種以前互不相容的自然定律的合一論》(Accorddeplusieursloisnaturellesquiavaientparujusqu'iciincompatibles)中，莫佩爾蒂提出，光折射的路徑，從一種介質到另一種介質，是作用量的最小值。按照這論點，如前圖，假設光線從折射率為的介質１折射於折射率為介質２，則作用量為
其中，是光線的質量。雖然光線並沒有質量，這變數對於結果沒有任何影響，可以被忽略。
取作用量對於變數的導數，設定為零，經過一些運算，可以得到 。
請注意，這結果與牛頓的光粒子理論相符合；但是，與費馬得到的結果南轅北轍，大不相同。
