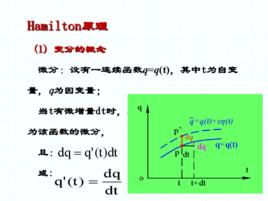
定義
亦稱最小作用原理.力學中的一個變分原理.拉格朗日函式L是質點組的動能與勢能之差,即L=T-V。
哈密頓原理是以變分為基礎的建模方法,設系統的動能為T,勢能為V,非保守力的虛元功為δw時,則哈密頓原理可以表示為
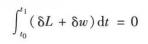 哈密頓原理
哈密頓原理哈密頓原理常用來建立連續質量分布和連續剛度分布系統(彈性系統)的動力學模型。
哈密頓原理斷言:在一切容許的運動中,質點組的真實運動滿足積分
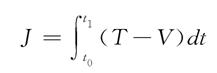 哈密頓原理
哈密頓原理有極值的必要條件δJ=0.
如同一般變分原理一樣,從哈密頓原理可以等價地推出相應的質點組的運動方程,通常是微分方程.如果力學系統處於靜力平衡穩定狀態,則因動能為零,位能與時間無關,哈密頓原理轉化為最小位能原理:
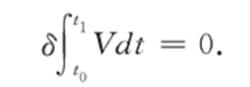 哈密頓原理
哈密頓原理在力是保守力的情況下,對任何有限粒子組,對於更一般的動力系統以及連續介質,這一原理的推廣同樣適用.哈密頓原理還可推廣到電磁學、量子學說以及相對論中的基本定律.量子學說的創立者普朗克(Planck,M.)這樣評價哈密頓原理,“物理學中最崇高且最為人們殷切追求的目標,是把業已觀察到並行將觀察到的一切自然現象縮並成單獨一個原理……在那些標誌著過去幾百年物理科學成就的,多少帶有一般性的定律中,最小作用原理,就其內容和形式而論,可能最接近於理論研究上這一理想的最終目標.”
原理的證明
因為
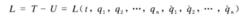 式1
式1所以
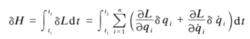 式2
式2由分部積分關係並考慮到固定點A,B的變分δq1為零,有
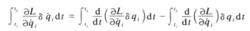 式3
式3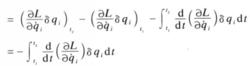 式3
式3代人式2,得
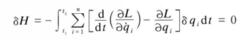 哈密頓原理
哈密頓原理根據變分原理,歐拉方程為
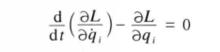 式5
式5式5就是在勢力作用下的拉格朗日方程,即當
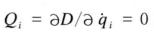 哈密頓原理
哈密頓原理的情況.在對積分極限加上一些限制條件,使真實運動的作用量的二階變分δ²H為正值時,真實運動作用使H取極小值,此原理稱為哈密頓最小作用量原理.因而拉格朗日方程5是哈密頓原理的充要條件.
當完整質點系統所受主動力中包含有勢力和非有勢力兩部分時,哈密頓原理有如下形式:
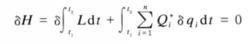 式6
式6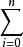 哈密頓原理
哈密頓原理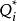 哈密頓原理
哈密頓原理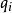 哈密頓原理
哈密頓原理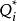 哈密頓原理
哈密頓原理式中,δ為非有勢力的虛功之和.上式與一般形式的拉格朗日方程
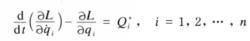 式7
式7是等價的,
當
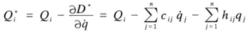 式9
式9時,式7即是式
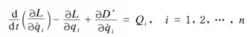 哈密頓原理
哈密頓原理