基本內容
現實生活中，人們經常見到一些網路，如鐵路網、公路網、通信網、運輸網等等。這些網路有一個共同的特點，就是在網路中都有物資、人或信息等某種量從一個地方流向另一個地方，如何安排這些量的流動以便取得最大效益是一個很有意義的實際問題。50年代福特（Ford）、富克遜（Fulkerson）建立的“網路流理論”，是網路套用的重要組成部分 。
最大流
給定指定的一個有向圖，其中有兩個特殊的點源S(Sources)和匯T(Sinks)，每條邊有指定的容量(Capacity)，求滿足條件的從S到T的最大流(MaxFlow)。
最小割
割是網路中定點的一個劃分，它把網路中的所有頂點劃分成兩個頂點集合S和T，其中源點s∈S,匯點t∈T。記為CUT(S,T)，滿足條件的從S到T的最小割（Min cut）。
相關定理
定理一：
如果f是網路中的一個流，CUT(S,T)是任意一個割，那么f的值等於正向割邊的流量與負向割邊的流量之差。
最大流最小割定理證明：
設X和Y是網路中的兩個頂點集合，用f（X,Y）表示從X中的一個頂點指向Y的一個頂點的所有弧（弧尾在X中，弧頭在Y中：
下列結論成立：
最大流最小割定理如果X∩Y=
，那么：f(X,(Y1∪Y2))=f(X,Y1)+f(X,Y2) ，f((X1∪X2),Y)=f(X1,Y)+f(X2,Y) 成立。根據網路流的特點：
如果V既不是源點也不是匯點，那么： f({V},S∪T)-f(S∪T,{V})=0；任何一個點，流入的與流出的量相等。
如果V是源，那么：f({V},S∪T)-f(S∪T,{V})=f。
對於S中的所有點V都有上述關係式，相加得到：f(S,S∪T)-f(S∪T,S)=f 。
又因為： f(S,S∪T)-f (S∪T,S)= (f(S,S)+f (S,T))-(f(S,S) +f (T,S))= f(S,T)- f(T,S)，
所以：f= f(S,T)- f(T,S) 定理得證 。
推論一：
如果f是網路中的一個流，CUT(S,T)是一個割，那么f的值不超過割CUT(S,T)的容量。
推論二：
網路中的最大流不超過任何割的容量。
定理二：
在網路中，如果f是一個流，CUT (S,T)是一個割，且f的值等於割CUT(S,T)的容量，那么f是一個最大流， CUT(S,T)是一個最小割。
證明：
令割CUT（S,T）的容量為C，所以流f的流量也為C。假設另外的任意流f1，流量為c1，根據流量不超過割的容量，則c1<=c,所以f是最大流。 假設另外的任意割CUT（S1,T1），容量為c1，根據流量不超過割的容量，所以有c1>=c,故，CUT（S,T）是最小割。
定理結論
在任何的網路中，最大流的值等於最小割的容量 。
結論一：
最大流時，最小割cut(S,T)中，正向割邊的流量=容量，逆向割邊的流量為0。
結論二：
在最小割cut(S,T)中：
源點s屬於S。
如果i屬於S，結點j滿足： 有弧,並且c [i,j] >f [i,j] ,或者有弧,並且f [i,j] >0,那么j屬於S。否則不是最小割。 即從s出發能找到的含有殘留的點組成集合S，其餘的點組成集合T。
1.源點s屬於S。
2.如果i屬於S，結點j滿足： 有弧,並且c [i,j] >f [i,j] ,或者有弧,並且f [i,j] >0,那么j屬於S。否則不是最小割。 即從s出發能找到的含有殘留的點組成集合S，其餘的點組成集合T。
套用舉例
問題描述：
最大流最小割定理
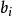最大流最小割定理 最大流最小割定理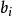 最大流最小割定理某軟體公司有n個可選的程式項目，其中第i個項目需要耗費資金
元，開發成功後可以獲得的收益為元。程式項目之間不是獨立的：開發第i個項目的前提條件是必須先開發出一些其他的項目，這些項目成為第i個項目的“前驅項目”。已經給出所有項目的和以及前驅項目，請幫助該公司從這n個程式項目中選擇若干個進行開發，使獲得的總收益最大。
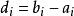最大流最小割定理
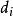最大流最小割定理 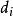最大流最小割定理分析：令 ，淨收益。A={i| >=0}:可以獲得利潤的項目集合。 B={i| <0}：虧損的項目集合。
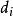最大流最小割定理 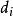最大流最小割定理構造網路圖： G=（V，E，C）。
1、兩類頂點：N+2個點：源點s個匯點t，第i個項目點vi。
2、三種弧：如果i∈A，存在弧<i,t>,容量為
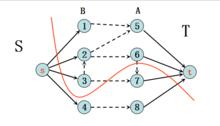圖1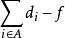
最大流最小割定理構造割cut（S，T），如果i∈T，則i的前驅j∈T。割對應一種實驗方案。最大收益為 。
